|
|
Presentazione del corso

Le presentazioni dei testi scolastici sono di solite noiosissime. Lo sono ancor di più quando si pretende di disquisire in termini teorici di questioni pedagogiche. Per evitare questo rischio abbiamo pensato di riproporre le domande e le osservazioni scaturite dal confronto con un gruppo di docenti che ha avuto modo di seguire il nostro lavoro e di leggere le bozze quando l'opera era ancora "in cantiere". Domande semplici e concrete. E risposte altrettanto semplici e concrete.
A chi si rivolge il corso?
Il corso copre tutti gli argomenti contemplati dai nuovi programmi per il primo biennio dei licei. Come sapete, i nuovi programmi prevedono alcune novità. Ad esempio danno uno spazio di rilievo alla rappresentazione di funzioni nel piano cartesiano (facendo anche uso di strumenti informatici) e al calcolo delle probabilità. Abbiamo cercato di valorizzare tali contenuti integrandoli in modo organico in un percorso didattico credibile.
Qual è la struttura del corso?
Il corso si articola in tre volumi: Algebra 1, Algebra 2 e Geometria. Più un corredo di schede di verifica raccolte in un volumetto per l'insegnante.
Qual è l'obiettivo principale che vi siete dati nello scrivere un nuovo corso di matematica?
Questo è un punto cruciale. Se vogliamo parlare francamente, dobbiamo partire dalla constatazione che il grado di preparazione matematica in Italia è del tutto insoddisfacente, è decisamente al di sotto di quella preparazione di base che il complesso mondo tecnologico richiederebbe. Non ce lo dicono solo le statistiche della Comunità Europea (che ci pongono agli ultimi posti), ce lo dice l'esperienza quotidiana: i ragazzi, in gran parte, hanno difficoltà con la matematica. Ma il problema, è chiaro, dipende dal modo in cui la matematica viene proposta. Dipende, cioè, da noi.
Il problema è che troppo spesso la lezione di matematica consiste nel mostrare delle tecniche risolutive senza che sia matura, nei ragazzi, la reale comprensione del significato, del senso degli oggetti matematici che entrano in gioco. Troppo spesso ci si fossilizza nel proporre esercizi meccanici, in particolare in campo algebrico, che lo studente affronta, come una sorta di apprendista stregone, manipolando formule e simboli senza capire qual è il loro scopo. Allora, se si accetta questa premessa, l'obiettivo principale è quello di proporre una matematica comprensibile. Legata ai sensi, alla sperimentazione, all'intuizione, alla verifica di laboratorio. E una matematica che appassioni l'allievo in un percorso di studio e di ricerca. Naturalmente non è affatto semplice raggiungere tale obiettivo e si può discutere sulle strategie da adottare.
Quali strategie avete adottato per proporre una matematica "comprensibile"?
Lo studente ha a disposizione due strumenti fondamentali per capire: gli esempi che si trovano alla fine di ogni paragrafo e le attività di laboratorio alla fine di ogni capitolo.
Gli esempi sono veramente numerosi, più di quanti siano normalmente proposti nei libri di testo. E hanno due scopi. Il primo è naturalmente quello di mostrare l'applicazione di tecniche o di regole (si tratta dei tipici esercizi svolti). Ma altri hanno la funzione di mettere a fuoco i nuovi concetti, di dare senso alle tecniche introdotte.
Potete chiarire in cosa consiste questo secondo tipo di esempi?
Riferiamoci a un caso concreto. Uno dei primi esempi proposti quando si introduce il calcolo letterale è questo:
E' vero che la somma di tre numeri naturali consecutivi è sempre un multiplo di tre?
Si mostra che l'affermazione è vera in alcuni casi particolari, ad esempio 1+2+3=6 oppure 12+13+14=39. Ma si fa riflettere l'allievo sul fatto che la verifica di uno, due, … mille casi, non significa provare l'affermazione in generale. Per ottenere questa prova "generale", che possa applicarsi a tutte le infinite terne di numeri consecutivi, abbiamo bisogno del simbolismo letterale. Non c'e altro modo. Solo la scrittura formale
n + (n+1) + (n+2) = 3(n+1)
è in grado di dominare il caso generale. Qui il calcolo simbolico, cioè il calcolo "con le lettere", trova la sua motivazione, il suo significato profondo. Naturalmente non basta un solo esempio e infatti se ne propongono vari e di varia natura.
Solo riflettendo su esempi di questo tipo l'allievo coglierà la portata enorme del calcolo letterale. Per lui sarà un delicato passaggio di maturazione in termini di astrazione.
Troviamo nel testo anche degli esercizi che vadano in questo senso?
Certamente, e parecchi. Alcuni semplici, altri meno semplici. Quelli più impegnativi sono contrassegnati dal numero su fondo arancione. Ma, degli esercizi, avremo modo di riparlare.
Quali ambienti informatici proponete per le attività di laboratorio?
Utilizziamo Derive nei volumi di algebra e Cabri, nella versione 2D e 3D, nel volume di geometria.
Vedo che le schede per le attività di laboratorio sono veramente corpose, parecchie pagine per ogni capitolo. Qual è il loro scopo?
Lo spazio dato alle attività di sperimentazione è effettivamente notevole. Nella nostra ottica le schede di laboratorio non sono una specie di abbellimento messo alla fine di qualche capitolo per assecondare una certa moda o per poter dire in copertina che si usa Cabri. No, per noi hanno un ruolo organico. Diamo al docente un segnale forte: se vuoi, puoi affrontare tutti i contenuti con la mediazione e il supporto di questi formidabili ambienti. Le tante attività vanno quindi a coprire tutti i contenuti proposti in fase teorica.
Quindi il vostro testo si rivolge solo ai docenti che fanno un uso massiccio dell'informatica?
Tutt'altro. Anche il docente meno propenso all'uso del laboratorio potrà gradualmente avvalersi delle attività che ritiene più opportune. Solo offrendo un percorso organico si può coinvolgere un ampio numero di docenti: devono infatti essere convinti dell'efficacia didattica di questo percorso. Bisogna mostrare, in attività concrete, che ambienti come Cabri e Derive possono migliorare radicalmente il modo in cui proponiamo i tradizionali contenuti.
Perché ritenete così importanti le attività di laboratorio? Tutto sommato si può far matematica anche senza fare "esperimenti".
La tecnologia consente oggi un modo diverso di apprendere i concetti della matematica. Pensiamo al concetto di funzione. Possiamo darne una definizione formale nel contesto molto astratto della teoria degli insiemi. Ma una definizione serve a poco se non se ne intuisce il significato. Immaginate però che l'allievo abbia a disposizione Derive. Potrà facilmente generare delle tabelle in cui appare con chiarezza la corrispondenza tra gli elementi di due insiemi. Con il semplice comando
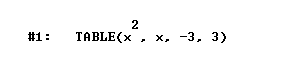
genererà la tabella dei valori reali x2 con x che va da -3 a 3 (con passo di una unità); otterrà cioè la tabella seguente in cui ad ogni valore x a sinistra è associato il corrispondente valore x2 a destra
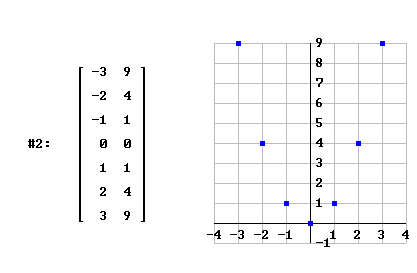
E potrà immediatamente rappresentare graficamente la tabella nella finestra grafica 2D di Derive, ottenendo un grafico "discreto", per punti. Grafico che, peraltro, potrà "impaginare" con una scala opportuna sui due assi (diversa sui due assi). Sarà poi abbastanza naturale chiedersi se è possibile cambiare il "passo" con cui si va da -3 a 3. Basterà considerare un nuovo parametro nel nostro comando Table. Ad esempio per avere un incremento di 0,5 darà il comando
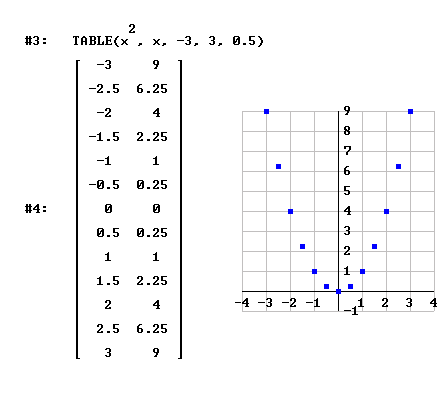
Mentre opera l'allievo si renderà conto che riducendo via via il passo si ottiene un grafico che gradualmente diventa continuo.
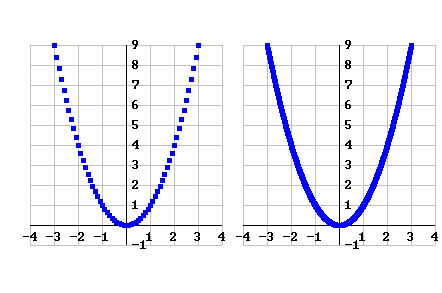
Potrà naturalmente "giocare" con i parametri in entrata nel comando Table, sostituendo ad esempio x2 con x+1. Potrà, da un certo momento in poi, cominciare a ragionare con la sua testa. Potrà fare dei suoi esperimenti. Potrà verificare delle semplici congetture (se faccio così mi aspetto che succeda questo…). Sarà direttamente coinvolto. Anche emotivamente.
Ritenete importante l'aspetto del coinvolgimento emotivo dell'allievo?
Sì, decisivo. La matematica o ti appassiona o ti fa paura.
Mi sembra che stiate delineando un metodo didattico in cui il momento dell'intuizione e della sperimentazione precede quello della formalizzazione. E' così?
Sì, è così. Almeno in tutti i casi in cui è possibile. La questione della formalizzazione è piuttosto delicata. Va affrontata con equilibrio. Non c'è matematica senza formalizzazione. Tra gli obbiettivi fondamentali che l'allievo dovrebbe raggiungere c'è la capacità autonoma di dare significato a definizioni formali, di seguire i passi formali di semplici dimostrazioni, di usare egli stesso dei livelli di formalizzazione per rappresentare con un modello matematico problemi reali. Questo però non significa proporre tonnellate di formalizzazione fin dai primi capitoli (tra l'altro in quell'ambito astrattissimo che è la teoria degli insiemi). Ci vuole gradualità. Servono mediazioni didattiche, come le attività di laboratorio. E molti esempi concreti.
Perché, per tracciare grafici, non avete utilizzato Excel che è molto diffuso nelle scuole?
Excel è una delle scelte possibili se ci limitiamo a tracciare grafici. Abbiamo preferito però proporre un unico ambiente che integri calcolo numerico, calcolo simbolico e grafica (2D e 3D). Excel, per quanto sia un gran bel programma, non appartiene a quella categoria di software che vengono chiamati CAS (Computer Algebra System) cioè a quegli ambienti come Derive, o Mathematica per citarne un altro, che dispongono di un "motore algebrico" in grado di fornire risulti esatti, simbolici. Per capirci, se digiti in una cella a formato numerico di Excel le espressioni
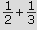 oppure oppure 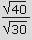
(precedute dal segno di uguale) otterrai invariabilmente dei risultati approssimati cioè otterrai rispettivamente
0,833333 e 1,154701
Se invece semplifichi le stesse espressioni con Derive otterrai i valori simbolici
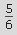 e e 
che, se vorrai, potrai approssimare con un'accuratezza arbitraria (ad esempio con 1000 cifre decimali). Non è una differenza da poco. Operando con Derive diventa subito chiara la differenza concettuale tra simbolico e numerico (ovvero tra valori esatti e valori approssimati). Poi con Derive puoi operare simbolicamente su espressioni algebriche, ad esempio
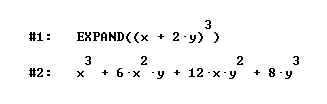
Oppure risolvere simbolicamente equazioni
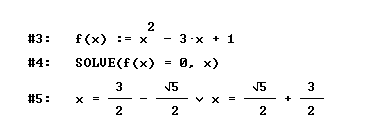
Potendo naturalmente approssimare le soluzioni
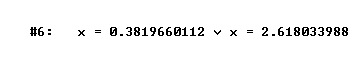
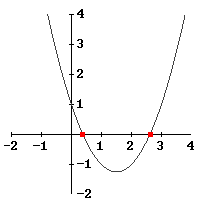 L'allievo, inoltre, potrà tracciare il grafico della funzione che si trova al primo membro dell'equazione semplicemente selezionandola e facendo clic sul relativo pulsante della finestra grafica. Si renderà conto così che le due soluzioni trovate sono le ascisse dei punti in cui il grafico taglia l'asse delle x. L'allievo, inoltre, potrà tracciare il grafico della funzione che si trova al primo membro dell'equazione semplicemente selezionandola e facendo clic sul relativo pulsante della finestra grafica. Si renderà conto così che le due soluzioni trovate sono le ascisse dei punti in cui il grafico taglia l'asse delle x.
Nel corso di algebra fate un ampio uso dei grafici cartesiani, fin dal primo anno. Alcuni docenti potrebbero trovarlo prematuro.
Si tratta di una scelta meditata, tra l'altro in linea con le indicazioni dei nuovi programmi. Tracciare un grafico a partire da una tabella è molto semplice, i ragazzi sanno farlo fin dalla scuola media. Non c'è bisogno di conoscere l'analisi o la geometria analitica. Perché non utilizzare grafici ogni volta che ci fa comodo? Per nostra fortuna non dovremo più tracciarli su fogli a quadretti o su carta millimetrata: la tecnologia sdrammatizza anche l'aspetto più noioso consistente nell'individuare con precisione i punti. Con Derive o con Cabri sarà un gioco tracciare grafici. In molte questioni algebriche l'appoggio visivo di un grafico vale più di mille parole.
Per di più, a partire dalla versione 6.0, Derive dispone delle cosiddette "slider bar" che rendono dinamici i nostri grafici. Potremo ad esempio studiare una famiglia parametrica di curve, come y=kx2: faremo variare k mediante un cursore a scorrimento (slider bar) e vedremo in tempo reale come varia il grafico parabolico. Oppure potremo discutere graficamente un'equazione parametrica. Insomma abbiamo uno strumento didattico veramente potente. La stessa nozione di parametro, tutt'altro che scontata per i ragazzi, assume una sua concretezza.
Nel secondo volume c'è un capitolo dedicato ai numeri complessi e al teorema fondamentale dell'algebra. Sono argomenti piuttosto avanzati che tradizionalmente non vengono trattati nel biennio (e, spesso, nemmeno nel triennio).
Il capitolo sui numeri complessi è breve e può, a giudizio del docente, essere saltato senza pregiudicare la comprensione dei capitoli successivi; inoltre i numeri complessi sono trattati ad un livello elementare (senza far ricorso alla forma trigonometrica e utilizzando solo le tecniche algebriche di fattorizzazione già acquisite). Il teorema fondamentale dell'algebra non viene naturalmente dimostrato ma la portata teorica del suo enunciato può essere tranquillamente compresa dallo studente del biennio. Perché dovremmo nascondere ai ragazzi quei pochi risultati veramente fondamentali concernenti la teoria delle equazioni algebriche se sono alla loro portata? Perché occuparci solo di tecniche risolutive, affrontando ad esempio classi molto particolari di equazioni algebriche di grado superiore al secondo (che ben difficilmente saranno poi incontrate nella pratica scientifica), e omettere completamente il quadro teorico?
Un problema analogo si pone per la questione della risolubilità per radicali. Perché non dire allo studente che per le equazioni di terzo e quarto grado esistono delle formule risolutive (che sono sì piuttosto complesse, tanto che non vengono trattate, ma che possono essere facilmente implementate in algoritmi eseguibili da un computer) mentre invece non esiste una formula generale per radicali per le equazioni di grado superiore al quarto?
La nostra impressione è che l'approccio alla teoria delle equazioni algebriche che si è sedimentato nel corso di oltre quarant'anni di pratica didattica (sostanzialmente incentrato sull'idea di produrre equazioni che lo studente potesse risolvere) è oggi entrato in crisi. Oggi con Derive, e con qualsiasi CAS, possiamo risolvere simbolicamente equazioni di terzo e quarto grado mentre per le equazioni di grado superiore al quarto, se si escludono classi particolari, gli stessi ambienti, non potendo fornire soluzione simboliche, ci forniscono soluzioni numeriche approssimate (con un grado arbitrario di accuratezza). E allora ci sembra veramente importante che oggi l'allievo sia in grado di capire la differenza tra soluzione simbolica (esatta, per radicali) e soluzione numerica approssimata ed abbia un minimo di consapevolezza del quadro teorico generale.
E' per questo motivo che date un certo spazio alla risoluzione approssimata di equazioni?
Sì, lo studente dovrebbero rendersi conto che esistono algoritmi per risolvere numericamente qualsiasi equazione algebrica; noi proponiamo il metodo di bisezione (che è semplice e intuitivo) e mostriamo come possa essere implementato con Derive. Non è certo il metodo più efficiente ma non è questo il punto. Quello che conta è capire che se rinunciamo alla ricerca di soluzioni simboliche non c'è alcun problema a risolvere equazioni. Non è una cosa da poco. E' un fatto che ha la stessa portata teorico-pratica (e forse di più) della formula risolutiva per le equazioni di secondo grado su cui tanto insistiamo. Formula, detto per inciso, che acquista agli occhi dei ragazzi il suo spessore teorico proprio quando diventano coscienti che non esistono formule simili per gradi superiori al quarto.
I capitoli di statistica e calcolo delle probabilità sono molto ampi così come lo sono le relative schede di laboratorio. Siamo sicuri che il docente avrà il tempo di trattarli?
I nuovi programmi danno un rilievo considerevole alla statistica e al calcolo delle probabilità. Il docente dovrà fare delle scelte: dare maggiore spazio ad un curricolo di tipo geometrico-algebrico oppure ritagliarsi uno spazio per la matematica non deterministica. Noi riteniamo che il calcolo delle probabilità abbia un enorme valore formativo (certamente maggiore di alcuni argomenti algebrici che soffrono, a nostro giudizio, di una sorta di "ipertrofia" nella tradizione italiana). Comunque, chi scrive un testo per il biennio, deve prevedere diverse scelte e diverse impostazioni didattiche; perciò abbiamo cercato di proporre un percorso organico per chi voglia affrontare questi argomenti.
Ritenete che i volumi di algebra siano corredati da un sufficiente numero di esercizi?
Riteniamo di sì, con questa precisazione. Nella tradizione italiana viene proposto un numero di esercizi veramente enorme che non trova riscontro, ad esempio, nella manualistica in lingua inglese. Il testo di matematica rischia di diventare sostanzialmente un grande eserciziario. La nostra impressione è che se dai dieci o venti esercizi alla volta non avrai poi il tempo di correggerli e di discuterli con i ragazzi: serviranno a poco. Saranno un puro e semplice esercizio meccanico.
Ora noi non abbiamo certo rinunciato a proporre esercizi il cui unico scopo è verificare l'acquisizione di una tecnica. Ce ne sono parecchi. Tra l'altro oggi per un autore è diventato molto facile produrre "in serie" esercizi di tipo meccanico; ma proprio la serialità degli esercizi è un segno della loro intrinseca debolezza. I programmi per il calcolo simbolico, come Derive, hanno messo a nudo questa situazione: se un esercizio può essere svolto da una macchina allora in quell'esercizio non c'è intelligenza. Non c'è intelligenza degli oggetti matematici che entrano in gioco, non c'è ricerca della soluzione, non c'è significato: c'è solo l'esecuzione di un algoritmo, di una procedura a livello sintattico. Ad esempio: è ben diverso risolvere un'equazione, per così dire, "nuda e cruda" oppure risolvere un problema, anche semplice, modellizzandolo con un'equazione.
Bene, è su questo secondo tipo di esercizi che abbiamo investito il nostro impegno. Esercizi, di vario tipo (anche di nuovo tipo) volti a verificare la reale comprensione dei concetti, a individuare relazioni, a trovare vie risolutive, a formulare congetture (e qualche volta a porsi nuovi problemi). Volti, insomma, a ragionare. E quando ci è sembrato necessario abbiamo inserito dei suggerimenti: perché un esercizio non deve mai essere troppo al di sopra delle possibilità dell'allievo.
Anche il corso di geometria razionale presenta delle novità sostanziali: in primo luogo il sistema di assiomi. Perché non proporre la solita assiomatica?
Secondo noi l'impianto assiomatico tradizionale, di stretta osservanza euclidea, non è il più conveniente sul piano didattico e pone qualche problema sul piano logico. Nell'impostazione tradizionale la nozione di congruenza viene fondata su quella di movimento rigido: due figure sono congruenti se posso muovere rigidamente l'una in modo da sovrapporla all'altra. In quest'ottica l'idea di movimento rigido viene assunta come primitiva, non definita. E' un modo di procedere direttamente derivato da Euclide; va detto che Euclide "trasporta" figure nel piano solo quando non può proprio farne a meno, essendo cosciente che il concetto fisico di movimento è estraneo alla geometria.
Un diverso punto di vista fonda invece la geometria sulla possibilità di misurare segmenti ed angoli. Ciò equivale all'assunzione di una sorta di "riga" ideale che ci consente di associare ad ogni coppia di punti la loro distanza (che è un numero reale) e di un "goniometro" ideale che ci consente di associare ad ogni angolo convesso la sua ampiezza (che, di nuovo, è un numero reale). E allora due segmenti o due angoli sono congruenti se hanno la stessa misura. La congruenza di triangoli viene poi definita a partire dalla congruenza di elementi corrispondenti (lati e angoli). E' un modo di procedere del tutto naturale. Noi, del resto, quando operiamo nel mondo reale, verifichiamo la congruenza degli oggetti misurando e non sovrapponendo.
E' questo secondo punto di vista quello che noi abbiamo assunto.
Quali sono le assiomatizzazioni della geometria elementare oggi considerate scientificamente corrette?
E' solo alla fine dell'ottocento che il sistema euclideo appare agli occhi dei matematici incompleto e insoddisfacente sul piano logico (ciò a causa dello sviluppo di geometrie "alternative", non euclidee, come la geometria iperbolica o la geometria ellittica che ponevano la necessità del massimo rigore nella formalizzazione delle assunzioni). Due sono le grandi sistemazioni della geometria euclidea ormai considerate classiche*. La prima, più vicina allo spirito di Euclide, è quella data da David Hilbert, nel 1899, nei suoi Grundlagen der geometrie (Fondamenti della geometria). La seconda è quella formulata dal matematico statunitense George David Birkhoff nel celebre articolo A set of postulates for plane geometry, based on scale and protractor del 1932.
Diciamo subito che né l'una né l'altra assumono l'idea di movimento rigido come primitiva. Nel sistema di Hilbert sono le nozioni di congruenza di segmenti e di angoli ad essere assunte come non definite (primitive) e ad esse si attribuisce significato, implicitamente, mediante un sistema di assiomi. Nel sistema di Birkhoff si assumono invece come primitive le nozioni di distanza tra due punti e di ampiezza di un angolo. La congruenza di segmenti ed angoli viene poi definita a partire dalla loro misura.
Il sistema di Hilbert è più vicino allo spirito euclideo perché non mette in gioco, fin dall'inizio, i numeri reali (cioè le misure di segmenti ed angoli). Tuttavia è troppo formale e complesso per essere proponibile sul piano didattico (e infatti nessun tentativo è stato fatto in questo senso). Al contrario il sistema di Birkhoff introduce fin dall'inizio i numeri reali (le misure) e si presta facilmente ad essere riformulato in un'assiomatica didatticamente proponibile. Dal sistema di Birkhoff derivano infatti la maggior parte dei sistemi assiomatici rivolti alla scuola nel mondo anglosassone (sistemi che sono ormai ampiamente collaudati). Anche la nostra assiomatica deriva da quella di Birkhoff.
* Vedi Piergiorgio Odifreddi, Divertimento geometrico - Le origini geometriche della logica da Euclide ad Hilbert, Bollati Boringhieri 2003, pag. 28-30.
Sono d'accordo che le nozioni di distanza tra due punti e di misura di un angolo sono intuitive ma sono altrettanto intuitive la nozione di movimento rigido e la definizione di congruenza come possibilità di portare una figura sull'altra. Non vi sembra?
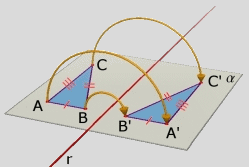 Sì è così e infatti anche noi le utilizziamo sul piano intuitivo (dicendolo però in modo esplicito). Tuttavia la definizione di congruenza come possibilità di portare una figura sull'altra pone qualche problema. Ad esempio per sovrapporre due triangoli speculari devo eseguire un ribaltamento cioè un movimento rigido che non è eseguibile nel piano. Allora dovremmo dire che per definire la congruenza nel piano abbiamo bisogno di una dimensione in più, dobbiamo operare nello spazio tridimensionale. Non è molto convincente.
Sì è così e infatti anche noi le utilizziamo sul piano intuitivo (dicendolo però in modo esplicito). Tuttavia la definizione di congruenza come possibilità di portare una figura sull'altra pone qualche problema. Ad esempio per sovrapporre due triangoli speculari devo eseguire un ribaltamento cioè un movimento rigido che non è eseguibile nel piano. Allora dovremmo dire che per definire la congruenza nel piano abbiamo bisogno di una dimensione in più, dobbiamo operare nello spazio tridimensionale. Non è molto convincente.
 E anche così facendo non risolveremmo il problema che si riproporrebbe per la congruenza nello spazio: è facile costruire due solidi speculari (simmetrici rispetto ad un piano), quindi congruenti, che tuttavia non sono sovrapponibili con un movimento rigido fisicamente realizzabile nello spazio. Anche in questo caso avremmo bisogno di una dimensione in più cioè di una quarta dimensione. Ma qui l'intuizione viene meno. E anche così facendo non risolveremmo il problema che si riproporrebbe per la congruenza nello spazio: è facile costruire due solidi speculari (simmetrici rispetto ad un piano), quindi congruenti, che tuttavia non sono sovrapponibili con un movimento rigido fisicamente realizzabile nello spazio. Anche in questo caso avremmo bisogno di una dimensione in più cioè di una quarta dimensione. Ma qui l'intuizione viene meno.
C'è poi un'altra questione. Nei moderni corsi di geometria si sente il bisogno di sviluppare, ad un certo punto, una teoria delle isometrie cioè delle trasformazioni del piano (o dello spazio) che conservano le distanze. Ora la nozione di isometria formalizza nel contesto astratto della geometria proprio la nozione intuitiva di movimento rigido. Ecco perché non conviene porre la nozione di movimento rigido come primitiva, non definita: sarà una nozione che troverà una sua coerente definizione a partire dal concetto di distanza.
Quali sono i vantaggi di un'assiomatica basata sulla misura di segmenti e di angoli?
Oltre alla maggior coerenza di cui si è già detto, ci sono dei vantaggi di tipo didattico. C'è una semplificazione che appare evidente in molte "strettoie" presenti nell'impostazione tradizionale. Per citarne una pensiamo alla teoria delle grandezze che appare agli occhi di molti docenti pesante, scientificamente obsoleta, didatticamente improponibile (e infatti sono molti a saltarla lasciando però in questo modo un vuoto logico nel percorso di geometria razionale). Mettendo in gioco fin dall'inizio i numeri reali non avremo questi problemi.
Qualcuno potrebbe ritenere che anche l'introduzione dei numeri reali sia pesante e di difficile gestione sul piano didattico.
E' un obiezione legittima che abbiamo tenuto ben presente. Nel terzo capitolo del primo volume di algebra proponiamo una teoria "ingenua" dei numeri reali cercando di rimuovere, per quanto possibile, le intrinseche difficoltà teoriche. E abbiamo sottolineato, nello stesso capitolo, come l'ampliamento dell'insieme dei numeri razionali nei reali sia dettato, tra l'altro, dalla necessità di approdare ad una soddisfacente teoria della misura. D'altra parte i numeri reali sono alla base non solo del corso di geometria ma anche di quello di algebra. Non avrebbe senso infatti proporre la teoria delle equazioni di secondo grado (con tutto il relativo macchinario dei radicali) se il nostro obiettivo non fosse quello di cercare soluzioni simboliche nell'insieme dei numeri reali. Quindi dei numeri reali non possiamo fare a meno. Tanto vale mettere subito a fuoco questo nodo e utilizzare i numeri reali tutte le volte che semplificano il percorso didattico.
In che modo avete introdotto i numeri reali?
Nel modo più semplice: come numeri decimali limitati o illimitati, periodici o non periodici. Non abbiamo certo pensato di affrontare una rigorosa teoria dei numeri reali. Non lo si fa nemmeno nella maggior parte dei corsi universitari di analisi. Ogni volta che abbiamo utilizzato in modo intuitivo delle proprietà dei numeri reali lo abbiamo detto. Non bisogna aver paura di ricorrere all'intuizione quando necessario. L'importante è dirlo.
Alcuni docenti potrebbero obiettare che l'introduzione del concetto di distanza (e quindi dei numeri reali) alla base del castello geometrico vada contro lo spirito euclideo e vada in qualche modo a minare la purezza del discorso geometrico.
Si tratta naturalmente di un punto di vista legittimo (e fondato). Teniamo presente però che il nostro scopo non è né quello della "purezza" né quello di formare degli storici della matematica. Vogliamo proporre un corso efficace. Gli aspetti che più ci stanno a cuore dell'opera del grande Euclide sono l'impostazione ipotetico-deduttiva e l'assunzione degli enti geometrici come enti astratti. Insomma, ci stanno a cuore i fondamenti del pensiero razionale. E questo è ampiamente recepito anzi, direi, valorizzato da un impostazione più scorrevole, più fruibile. La matematica, del resto, non è un corpo fossilizzato ma un organismo vitale in continua rapida evoluzione sia sul fronte avanzato della ricerca sia sul piano della didattica. Algebra, numeri reali, piano cartesiano, grafici, algoritmi hanno ormai fatto la loro irreversibile irruzione in campo geometrico e non possiamo non tenerne conto.
Per di più abbiamo cercato di mantenere la scansione dei contenuti molto vicina a quella tradizionale: perciò il docente non farà fatica a riadattare il suo percorso didattico. Una volta gettati i fondamenti della geometria, una volta arrivati, diciamo, ai criteri di congruenza, gran parte delle dimostrazioni corrono nel solito modo (e in qualche caso in modo più lineare, vedi il teorema di Talete).
Un'altra caratteristica del corso di geometria che colpisce è la trattazione, in un gran numero di esempi, della geometria sulla sfera cioè di una geometria non euclidea. Non vi sembra che sia un discorso prematuro se rivolto a ragazzi che hanno già fin troppi problemi con i concetti della geometria euclidea?
No, al contrario. Il nostro scopo è infatti proprio quello di aiutare i ragazzi a capire (e a capire l'impianto della geometria euclidea). E a motivarli, ad appassionarli. Una delle difficoltà maggiori in un corso di geometria razionale consiste nel rendere consapevole lo studente della necessità del rigore formale nel corso di una dimostrazione. Per i ragazzi molte proprietà sono scontate, intuitivamente evidenti. Il rigore appare ingiustificato, un peso inutile, un esercizio noioso. Non sentono la necessità di dimostrare.
 Il discorso cambia se si rendono conto che esistono modelli geometrici alternativi, del tutto comprensibili, in cui le ordinarie proprietà vengono a cadere. Le proprietà che davi per scontate e che consideravi assolute, che ti apparivano banali, acquistano una loro relatività e quindi interesse. Ecco perché ha un gran valore didattico mostrare un ambiente geometrico in cui due rette si incontrano sempre (e per di più in due punti), in cui per i poli di una retta passano infinite perpendicolari alla retta, in cui la somma degli angoli di un triangolo è sempre maggiore di 180° (e per di più varia da triangolo a triangolo), in cui il luogo dei punti equidistanti da una retta è una coppia di circonferenze, in cui figure simili sono anche, necessariamente, congruenti.
Il discorso cambia se si rendono conto che esistono modelli geometrici alternativi, del tutto comprensibili, in cui le ordinarie proprietà vengono a cadere. Le proprietà che davi per scontate e che consideravi assolute, che ti apparivano banali, acquistano una loro relatività e quindi interesse. Ecco perché ha un gran valore didattico mostrare un ambiente geometrico in cui due rette si incontrano sempre (e per di più in due punti), in cui per i poli di una retta passano infinite perpendicolari alla retta, in cui la somma degli angoli di un triangolo è sempre maggiore di 180° (e per di più varia da triangolo a triangolo), in cui il luogo dei punti equidistanti da una retta è una coppia di circonferenze, in cui figure simili sono anche, necessariamente, congruenti.
Va detto, inoltre, che il modello alternativo al piano euclideo che abbiamo adottato - la geometria sulla superficie di una sfera - ha una grande evidenza intuitiva. Tutte le proprietà sono ricavate in modo informale, sperimentale. Anche l'aspetto più delicato, consistente nel convincere i ragazzi che è del tutto ragionevole considerare "rette" le circonferenze massime, è affrontato partendo da esperienze concrete, partendo dai sensi (si utilizza anche un dispositivo meccanico). E i ragionamenti sviluppati sono sempre molto semplici, direi alla portata di uno studente di terza media.
Ci si avvale infine di uno strumento formidabile come Cabri 3D, per cui viene a cadere la difficoltà della rappresentazione grafica. Sarà facile, ad esempio, costruire dei triangoli sferici (per di più dinamici).
Nel vostro corso di geometria c'è un riferimento costante all'intuizione, all'esperimento, a modelli concreti. Ricorrete anche a immagini fotografiche di oggetti del mondo reale. Ancora una volta l'impostazione didattica è quella in cui il momento dell'intuizione precede quello della formalizzazione?
Esattamente. Non a caso il volume si apre con una citazione di Federico Enriques in cui si sottolinea come l'esperimento debba porsi alla base della geometria.
Questo è anche lo scopo delle attività con Cabri?
Sì, naturalmente. Prima di studiare (a memoria?) l'enunciato di un teorema devi capirlo. Pensate ad esempio al teorema di Talete. Se l'allievo può operare concretamente con Cabri, misurando segmenti corrispondenti in una proiezione parallela (potendo inoltre, grazie alla calcolatrice, confrontare rapporti di misure), coglierà subito il significato del teorema. E probabilmente si chiederà anche il perché della proprietà che sta verificando sperimentalmente e sarà così psicologicamente disposto ad affrontare una dimostrazione formale.
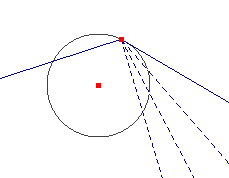 Facciamo un altro esempio. Pensate alla definizione formale di angolo alla circonferenza: dobbiamo annoverare, tra gli angoli, anche quelli che hanno un lato secante e l'altro tangente. La cosa spesso non convince i ragazzi. Se però l'allievo costruisce un angolo alla circonferenza "dinamico" potrà rendersi conto, trascinando con il mouse un lato dell'angolo, che la situazione contemplata dalla definizione è una situazione limite che può essere raggiunta gradualmente. E così coglierà il senso della definizione. Le potenzialità dinamiche di Cabri sono decisive per capire. Facciamo un altro esempio. Pensate alla definizione formale di angolo alla circonferenza: dobbiamo annoverare, tra gli angoli, anche quelli che hanno un lato secante e l'altro tangente. La cosa spesso non convince i ragazzi. Se però l'allievo costruisce un angolo alla circonferenza "dinamico" potrà rendersi conto, trascinando con il mouse un lato dell'angolo, che la situazione contemplata dalla definizione è una situazione limite che può essere raggiunta gradualmente. E così coglierà il senso della definizione. Le potenzialità dinamiche di Cabri sono decisive per capire.
Non vi sembra però che Cabri, in quanto ambiente operativo, allontani i ragazzi dall'astrazione?
No, anzi riteniamo che sia vero il contrario. La capacità di astrazione va conquistata con un lungo percorso.
Le figure di Cabri possono essere modificate (o, se preferite, trasformate) conservando sempre, però, le condizioni geometriche (o i vincoli) che abbiamo imposto nella loro costruzione. Questo è un aspetto cruciale che i ragazzi devono aver ben presente. Se ad esempio costruiamo un rombo con Cabri, dovremo imporre nella sua costruzione due condizioni di parallelismo (lati opposti paralleli) e una condizione di uguaglianza per due lati consecutivi. Ma, ecco il punto, la figura che otterremo - al contrario di quello che avverrebbe se disegnassimo su carta - sarà una figura dinamica: potremo deformarla utilizzando il mouse. E ciò accade perché le condizioni imposte nella costruzione lasciano ancora dei gradi di libertà al nostro rombo. Potremo modificare la lunghezza dei lati o variare l'ampiezza degli angoli. Basterà "afferrare" un vertice col mouse e trascinarlo. E' un'esperienza straordinaria, decisiva sul piano dell'apprendimento. La figura costruita è in realtà un modello generale (astratto) di rombo, rappresentativo di tutti i rombi. Un'esperienza simile non è producibile su carta: lì non c'è modo di trascinare punti!
Ma c'è qualcosa di più profondo. Se disegniamo su carta siamo costretti a introdurre più condizioni di quante ne siano richieste dalla definizione di rombo: dovremo fissare la lunghezza del lato e l'ampiezza di un angolo. Cadremo quindi in una costruzione particolare. Cabri invece, grazie al trascinamento, libera i ragazzi dai casi particolari, li spinge verso l'astrazione. Li spinge a cercare, sperimentando, quali proprietà si conservino, indipendentemente dalla situazione particolare, e quindi, in ultima analisi, quali proprietà discendano necessariamente dalle condizioni imposte nella costruzione. Cabri non è un semplice programma per disegnare: è un ambiente per sviluppare l'intuizione geometrica e il pensiero logico.
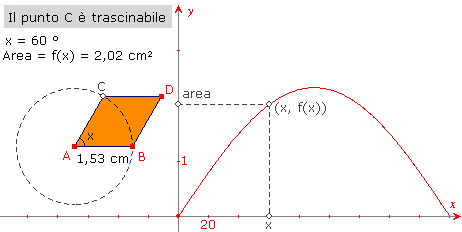
Pensate infine alla possibilità di collegare interattivamente una figura dinamica in cui varia una certa grandezza f(x) (ad esempio l'area) in funzione di un'altra grandezza x (ad esempio un angolo), al grafico cartesiano di f(x). Potremo anche evidenziare, sul grafico, il punto dinamico (x, f(x)). Avremo nello stesso foglio di lavoro due universi concettuali: quello geometrico e quello algebrico. Non è poco. E questa si chiama astrazione.
Sia i volumi di algebra sia quello di geometria sono costellati di note storiche. Inoltre nelle introduzioni ad ogni capitolo si fa cenno ai matematici che hanno contribuito allo sviluppo delle idee di cui ci si occuperà. Questa attenzione è motivata da ragioni didattiche?
Siamo coscienti che i riferimenti storici presenti nel testo sono assolutamente modesti e infatti stiamo pensando a qualcosa di più organico per il futuro. Abbiamo evitato di inserire qua e là delle isolate schede storiche (che a nostro giudizio sarebbero apparse come un "accessorio" trascurabile), mettendo invece in primo piano, nelle aperture dei capitoli, qualche elemento di storia della matematica. Con un intento ben preciso. Vorremmo che i ragazzi considerino la matematica come un processo evolutivo, tuttora impetuosamente in corso, denso di problemi, di difficoltà, di passaggi radicali e non come un disegno ormai compiuto che viene a loro svelato. Un processo parallelo allo sviluppo storico dell'uomo e alla sua capacità di comprendere il mondo. Alcune rivoluzioni concettuali hanno richiesto una maturazione del pensiero matematico lunga molti secoli. Non devono quindi meravigliarsi, i ragazzi, delle loro difficoltà. E non ne devono avere paura.
Ora che abbiamo un quadro abbastanza preciso del progetto didattico che è alla base del vostro testo, potete riassumere, in poche parole, gli obiettivi che vi siete dati?
Un progetto didattico efficace dovrebbe sviluppare la capacità di prendere decisioni in situazioni e contesti diversi, di adottare strategie alternative, di risolvere problemi reali. Dovrebbe puntare non solo al sapere operativo, su cui forse si insiste troppo, ma favorire la comprensione dei risultati e degli algoritmi. Dovrebbe legarsi al concreto e alla sperimentazione. Dovrebbe promuovere il pensiero autonomo. Dovrebbe guidare i ragazzi a rendere produttivi i loro errori, a procedere per approssimazioni successive, come ci insegna il pensiero informatico. Dovrebbe far apprezzare la bellezza della matematica, il piacere di capire, il piacere del gioco: la matematica come gioco.

|
|

