Circonferenze
Nella figura seguente vedete una circonferenza nel piano ellittico; potete trascinare i punti A e B. Una circonferenza nel piano ellittico viene definita nello stesso modo del piano euclideo: è il luogo dei punti equidistanti da un punto A (la distanza che entra in gioco è naturalmente la distanza ellittica). A è il centro della circonferenza e AB è il raggio della circonferenza. Notate che una circonferenza nel piano ellittico è costituita da due circonferenze euclidee antipodali (i cui punti antipodali sono identificati). Il raggio è naturalmente quello intriseco, è cioè un arco di circonferenza massima. Il massimo raggio di una circonferenza è uguale a p/2, poichè non esistono punti nel piano ellittico la cui distanza sia maggiore di p/2.
Nella figura seguente vediamo una circonferenza di centro A il cui raggio AB varia con continuità tra 0 e p/2. E' inoltre visualizzata la distanza ellittica Distance(A; B). Nella situazione limite in cui il raggio è uguale a p/2 le due circonferenze (euclidee) antipodali coincidono e dunque la circonferenza ellittica sembra coincidere con una retta ellittica (cioè con una circonferenza massima i cui punti antipodali siano identificati).
Tuttavia le cose non stanno esattamente così. Cominciamo con l'osservare che la formula che ci fornisce la lunghezza c di una circonferenza nel piano ellittico (sfera unitaria) è, quando il raggio r è minore di p/2, evidentemente la stessa della geometria sferica
c=2p sen r(vedi La geometria sulla sfera - Paragrafo 14).
Tale formula nella situazione limite di r=p/2
ci fornisce un valore per c pari a 2p. E ciò sembra in contraddizione col fatto che una circonferenza di raggio p/2 debba coincidere con una retta ellittica la cui lunghezza, lo sappiamo, è p. D'altra parte ci aspettiamo che la lunghezza della circonferenza debba aumentare con continuità fino a 2p, per poi cominciare a decrescere.
La figura seguente ci fornisce un suggerimento per risolvere la questione. Qui vediamo un punto B che si muove con continuità su una circonferenza (rappresentata da due circonferenze euclidee antipodali in rosso). Vediamo inoltre, in azzurro, la retta ellittica a che sembra separare le due circonferenze euclidee. Ma osservate il percorso del punto B: si trova sia al di sopra che al di sotto della retta a. Inoltre mentre il punto B descrive tutta la circonferenza, il punto A descrive due volte la retta a. Anche nella situazione limite in cui r=p/2 il punto B descrive due volte la retta a e dunque la lunghezza della circonferenza è in questo caso uguale a 2p (in accordo con la formula).
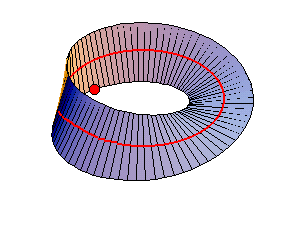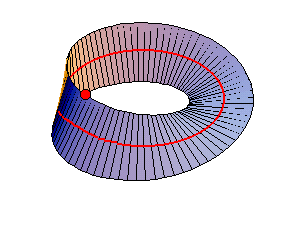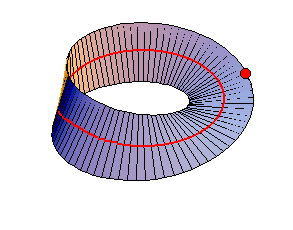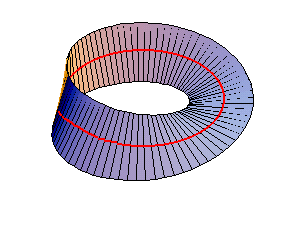Ci siamo anche resi conto che il piano ellittico non viene separato dalla retta a in due semipiani, come avverrebbe in geometria euclidea o in geometria sferica. Da questo punto di vista il piano ellittico assomiglia al nastro di Moebius che vedete nell'animazione.
La linea rossa sembra dividere a metà il nastro di Moebius, ma non è così. Il punto rosso che si muove lungo il bordo del nastro (costituito da un'unica linea curva) si trova sia da un parte che dall'altra della linea rossa (in realtà non ha nemmeno senso dire che si trova da una parte o dall'altra, riflettete). Il punto B che si muove sulla circonferenza nel piano ellittico si comporta nello stesso modo del punto in movimento sul nostro nastro di Moebius (vedi H. S. M. Coxeter, Non-euclidean geometry, parag. 6.53).
Esperimento Ritagliate una striscia rettangolare di carta, lunga e stretta, ad esempio 30 cm x 4 cm; tracciate in rosso, su entrambe le facce della striscia, il segmento che congiunge i due punti medi dei lati di 4 cm; incollate poi le estremità della striscia dopo aver ruotato di 180° uno dei lati di 4 cm. Otterrete così un nastro di Moebius. Provate ora a tagliare il nastro di Moebius lungo la linea rossa: vedrete che il nastro non si separa in due parti !