Le osservazioni fatte delle fluttuazioni del fondo cosmico concordano con uno spettro invariante in scala con un'ampiezza su scala dell'orizzonte dell'ordine di 10-4.
Nell'universo attuale il contributo alla densità è data principalmente dalla materia, ma nel passato era dominante la densità di energia. Nelle fluttuazioni adiabatiche la densità di materia varia in sincronia con le variazioni di densità di energia (la densità di radiazione risulterebbe costante con fluttuazioni isoterme), e sembrano più plausibili le fluttuazioni adiabatiche.
Le fonti principali di fluttuazioni di temperatura (oltre l'anisotropia di dipolo) su scala angolare ³ 5¢, nei modelli Wo = 1, sono le fluttuazioni del potenziale (scalare) gravitazionale (o fluttuazioni Sachs-Wolfe) e le perturbazioni adiabatiche.
Dalle anisotropie della radiazione di fondo cosmico possiamo scoprire molto riguardo alle formazioni ed evoluzioni delle fluttuazioni, e di come si sono evolute per diventare le strutture nell'universo da noi osservato. Lo spettro è particolarmente ricco su scala piccola (al di sotto del grado) dovuto alle oscillazioni prima che la materia diventasse neutra, quando le onde (acustiche) furono ``fissate'' molti parametri cosmologici, come Wo, il contenuto barionico WB e la costante di Hubble Ho. Quindi nella radiazione di fondo le anisotropie non solo rappresentano i ``semi'' delle prime strutture ma permetterebbero anche le misure di vari parametri cosmologici.
Ci sono indicazioni che le strutture di larga scala dell'universo si siano sviluppate da processi di instabilità gravitazionale dovuti a piccole perturbazioni primordiali nella densità di energia o delle oscillazioni acustiche spinte dalle forze gravitazionali. Queste fluttuazioni potrebbero essere state determinate da fluttuazioni quantistiche durante la fase inflazionaria.
Le regioni più dense collassarano sotto la propria attrazione gravitazionale. Questo processo di aggregazione è proporzionale alla scala delle fluttuazioni di densità.
Nel modello standard i fotoni che osserviamo non interagirono più con la materia da circa z = 1000, quando l'orizzonte di allora è sotteso da un angolo di 1o o multipolo l ³ 100, e solo su questa scala (angolare) o meno possono essere avvenuti processi fisici significativi, al di sopra di tale scala sarebbero stati oltre l'orizzonte.
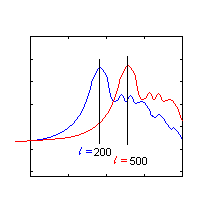
Dalla ``sfera'' dell'ultimo scattering a z = 1000 noi vediamo le perturbazioni di temperatura come delle anisotropie sia dalla modifica di energia nei fotoni lungo il loro viaggio verso di noi che dalle perturbazioni dei fotoni che ``salirono'' i pozzi potenziali. Per le onde lunghe di perturbazioni (di densità o potenziali) si manifestano come perturbazioni di temperatura che noi rileviamo come anisotropie su larga scala. Mentre i processi fisici della superficie stessa si manifestano come picchi (in particolare nello spettro intorno a l " 200 cioè q " .5¢).
Finchè i fotoni e i barioni erano accoppiati (principalmente dallo scattering di Compton) essi agivano come un ``plasma'' la cui pressione era fornita dai fotoni. Questo plasma subiva delle oscillazioni ``acustiche'' e con il crescere dell'orizzonte addensamenti di lunghezza sempre più grande riuscivano ad entrare. Appena l'addensamento entra esso collassa sotto la propria forza gravitazionale, fino a che la pressione dei fotoni ne risente e in tal modo inizia un'oscillazione che può essere descritta da un'equazione di un oscillatore armonico.
Si assume quindi che queste fossero perturbazioni di densità adiabatiche Gaussiane, il cui spettro all'entrata dell'orizzonte sia più o meno indipendente di scala e che Wo sia prossimo a 1 (nell'insieme fra 0 e 1).
Quando il ``plasma'' si raffreddó abbastanza da permettere ai protoni di catturare gli elettroni e formare l'idrogeno neutro, i barioni e la radiazione si ``separarono'', e i barioni non poterono più usufruire della pressione dei fotoni e quindi ``cascano'' per formare le strutture che osserviamo oggi. I fotoni intanto proseguono (interagendo solo gravitazionalmente) e le componenti di velocità e densità nelle oscillazioni si rilevano come anisotropie di temperatura. Più era denso una zona al momento di ricombinazione e più sara calda (quindi più brillante) al momento dell'osservazione.

Vediamo in figura 1 lo spettro di potenza angolare della RDFC, o anche spettro di potenza di anisotropia, Cl = < alm2 > (componente multipolo - armoniche sferiche), può essere raffigurata rispetto al numero di multipolo l, oppure rispetto a q, l'angolo sotteso, o anche formalmente rispetto al numero d'onda k (in tal caso si può trattare in modo simile sia lo spettro di potenza della materia Pmat (k) che quella della radiazione Prad (k)). Questi parametri sono legati fra di loro dalle funzioni
|
|
È standard lavorare in termini dei momenti di multipolo nell'anisotrropia della temperatura e si definisce
|
Se le fluttuazioni hanno una distribuzione Gaussiana sono allora univocamente specificati da Cl, che sono funzioni dei parametri cosmologici.
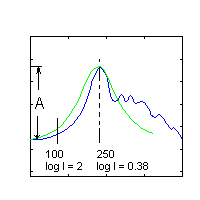
La figura 2 mostra lo spettro di anisotropie per il modello standard (con Wo = 1, h = 0.5 e H0 = 100 h km s-1 Mpc-1)
Gli elementi del grafico (alcuni li vedremo in dettaglio più avanti) sono:
La posizione del primo picco (nel modello Wo = 1) è ben determinato dalla geometria dell'universo. La curvatura fa divergere i raggi dalla superficie dell'ultimo scattering all'osservatore.
Il primo picco può essere approssimato da uno spettro di potenza costante (vedere Figura 2), più un picco lorentziano che possiamo esprimere analiticamente come:
|
|
Con l'evolversi dell'universo le perturbazioni su larga scala sono instabili, e ciò è dovuto alla propria gravità su scala di Jeans.
Su scala più piccola oscillano come onde; spinte sia dalla forza gravitazionale che dalla forza ``restauratrice'' di pressione. L'ampiezza del picco dipende dalla forza di restauro, quindi dal rapporto barioni-fotoni NB / Ng, mentre il potenziale dipende da quanto vicino era il tempo di equivalenza al tempo dell'ultimo scattering.
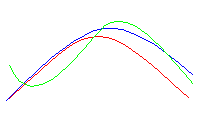
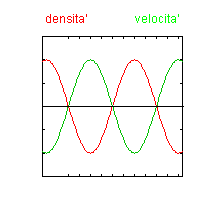
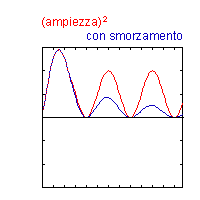
Il primo picco nello spettro di radiazione sarà quindi una perturbazione che ha attraversato l'orizzonte ed era alla massima densità al momento della ricombinazione, poi c'è un picco di sottodensità, e così alternandosi i picchi (perchè i picchi sono il quadrato della differenza di temperatura). Gli avallamenti sono invece dei massimi di velocità. (Vedere figura 3) Poichè la ricombinazione ha impiegato un tempo sufficiente per permettere lo smorzamento delle anisotropie troppo piccole, quindi con il crescere di l i picchi diminuiscono.
La scala fisica del primo picco è la grandezza dell'orizzonte al momento dell'ultimo scattering, che noi supponiamo dipenda dalla temperatura e quindi quasi sicuramente a z = 1000.
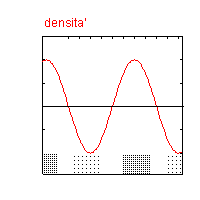
Se lo spettro di potenza fosse privo di caratteristiche si avrebbe uno scatter su una retta orizzontale, e sarebbe quindi privo di picchi.
Se il primo picco fosse spostato (nella figura 4 per esempio a l " 500) implicherebbe un universo più aperto, poichè la stessa scala fisica sottenderebbe una scala angolare minore.
La conversione dalla RDFC allo spettro di potenza della materia dipende molto dalla teoria adottata.
Due esempi, il modello CDM prevede una maggiore potenza su piccola scala e i modelli inflazionari aperti (Wo < 1 prevedono un cadere su scala del COBE. (Vedere figura 5)
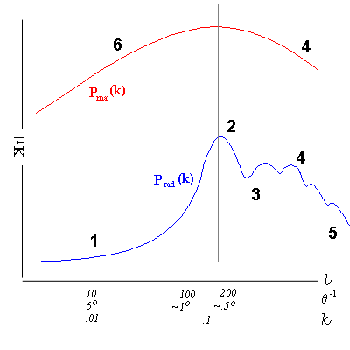
Si può confrontare la struttura su larga scala delle galassie (che, dopotutto, è una misura delle fluttuazioni di densità attuali) con la RDFC che sono le fluttuazioni di temperatura all'ultimo scattering.
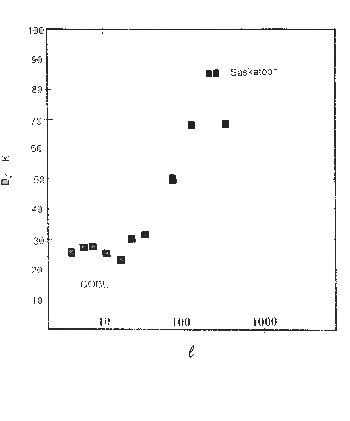
Vi sono stati moltissimi esperimenti negli ultimi anni per cercare di creare una mappa della RDFC, oltre COBE - sicuramente il più noto - ci sono stati anche FIRS, TENERIFE, SASKATOON (vedere [9] per un'analisi e confronto dei vari esperimenti fatti fino ad oggi.)
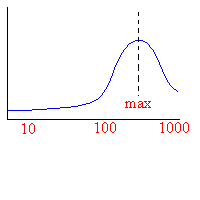
Una prima analisi dei dati sembra indicare (vedere figura 6) uno spettro di radiazione piatto su scala angolare grande, e un picco attorno ad un multipolo l " 250 corrispondente circa ad una scala angolare di 0.5o che è circa da 4 a 5 volte l'ampiezza della parte piatta. (Assumendo scartati contaminazioni del foreground.)
Vorrei confontare questo con un grafico (figura 9) che ho tratto da dati di White [10] per momenti di multipolo del modello CDM standard (Wo = 1, WB = 0.05 e n = 1) dove i momenti sono normalizzati per ottenere D10 = 1
I Cl sono di fatto una media pesata di una banda di multipoli, dove i pesi sono ``funzioni finestra'' (window function). Una migliore funzione di finestra dovrà essere centrata attorno a l con un'ampiezza di scarto quadratico medio Dl il più piccolo possibile. Usando armoniche sferiche si può abbassare la risoluzione spettrale Dl/ l di circa il 25 %. Una stima di Cl si ottiene prendendo una combinazione lineare dei pixel, facendo il quadrato e sottraendo il contributo dal rumore. Nel metodo chiamato Hauser-Peebles si stima invece con la media delle ampiezze quadrate dei diversi (2 l+ 1 ) coefficienti armonici sferici.
Concentrandosi sui dati da due esperimenti con le funzioni finestra più strette,1 COBE e Saskatoon, vediamo un fit plausibile con due varianti del modello Cold Dark Matter standard, con n = 1 e Wb = 0.05 come mostrato nelle figure delle ultime due pagine dove la linea solida è il modello piatto con L = 0.7 e la linea trateggiata il modello con h = 0.3.
I dati attuali del COBE sembrano in accordo con l'esistenza di un picco adiabatico, con una ricombinazione a z " 1000 e un universo neutro fino a z " 50, e lo spettro di potenza iniziale sembra essere invariante in scala.
A partire da un modello cosmologico, per esempio Friedmann-Lemaître, la costruzione di una teoria della formazione delle galassie, richiede delle scelte sui parametri. Per esempio decidere se sezioni dello spazio devono essere (cosmologicamente) curve o piatte, e come dev'essere la densità di materia. Un modello piatto concorda con l'inflazione, che è sicuramente una delle immagini migliori che abbiamo dell'universo primordiale. Dagli attuali dati osservativi il parametro di densità risulterebbe al di sotto di uno, ma potrebbe non essere accettabile (fra le altre cose implicherebbe che siamo degli osservatori privilegiati comparsi proprio mentre l'universo si sta allontanando dall'essere dominato dalla sua densità di massa).
Bisogna anche decidere quali sono i contributi principali alla massa dell'universo e la causa degli stress che hanno fatto si che la materia si raccogliesse nelle strutture osservate. Infine sarebbe un grande passo avanti capire che cosa sono i ``semi'' gravitazionali delle strutture. Si potrebbe assumere che si sviluppino senza bisogno di specificare le condizioni iniziali, come la turbolenza di un liquido che fluisce in un tubo sottoposto ad una instabilità esponenziale, altrimenti considerare la crescita gravitazionale delle fluttuazioni della massa in un universo in espansione sottoposto ad una instabilità a legge di potenza, in qual caso vi sono dei vincoli specifici sulle condizioni iniziali.
Nell'ambito del modello standard sembrano esserci vari motivi validi per assumere che l'universo primordiale avesse avuto ben presto una brevissima era di inflazione. Senza l'inflazione l'universo sarebbe o collassato o diventato vuoto nell'arco di breve tempo a meno che il parametro di densità non fosse estremamente vicino al valore di uno, mentre l'inflazione porta il parametro di densità a uno, pur partendo da un valore iniziale arbitrario.
C'è anche il tema della omogeneità e isotropia. Le fluttuazioni su scala comovente genera perturbazioni che spiegano bene la disomogeneità e anisotropia dell'universo osservabile, proprio perchè l'inflazione prevede una perturbazione di densità (adiabatica)
L'aspetto più attraente dell'inflazione è la possibilità che possa fornire la spiegazione dei semi perturbativi che hanno poi prodotto le strutture che oggi vediamo.
Certo che le teorie, anche le più attraenti, devono poi fare i conti con i dati osservativi. La quantità di dati sta aumentando enormemente. Si stanno facendo nuovi passi avanti nelle metodologie di osservazione e anche nell'analisi dei segnali per rilevare le strutture a larga scala.[3] Le più recenti confermano che a larga scala la distribuzione delle galassie sia omogenea e isotropa, mentre a scale più piccole c'è una gerarchia di strutture, vuoti, galassie isolate, gruppi e infine ammassi.
Qualsiasi teoria dovrà essere in grado di spiegare quello che osserviamo, e non solo grazie ad un ``fine tuning'' dei parametri. Nella conclusione dell'articolo di Fukugita [2] troviamo alcuni esempi delle sfide che le osservazioni di oggi pongono alle teorie dell'origine delle galassie e la loro distribuzione su larga scala.2
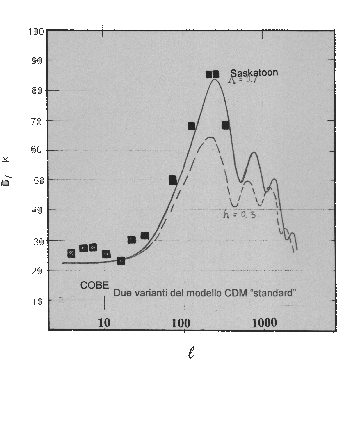
1 Nella stima dello spettro di potenza spesso si usano barre di errore sia verticali che orizzontali, dove le prime indicano incertezze dovute a rumore e varianza del campionamento mentre le ultime indicano eventuali contributi da altri momenti di multipolo.
2 Questa tesina è stata preparata con il sistema LATEX.


Last Update: February 5, 1999