Recursive formula for the ``components'' of a hyper-cube¹

A. De Paoli

Starting from considerations regarding the ``components'' of cubes in various dimensions we find a recursive formula H^m_n = 2 ·H^m_n-1 + H^m-1_n-1 which, incidentally, when generalized gives Euler's formula up to 3-d space and also establishes an analog of the formula for other spaces as well.

MSC 54B20, 03D20

Euler's formula, V - E + F = 2, gives a relationship between the vertices edges and faces of polyhedra. A cube has, in fact, 8 vertices, 12 edges and 6 faces. Let us call vertices, edges and faces ``components'' of the cube. Now a square has 4 edges, 4 vertices and one face (which is the square itself). The components of the line segment are two vertices and one edge, the line itself.

We may imagine a cube being generated by moving a square orthogonally with respect to the plane containing the square. The square, in turn, being produced by ``dragging'' a line segment (its length is one side of the square) along the plane a distance equal to its length. We can say the square has been ``generated'' by the line segment. But the line segment itself may be considered as the one dimensional analog of the square, ``generated'' in turn by a point.

Going in the other direction, towards higher dimensions, with the cube we can generate a 4-dimensional hyper-cube, and so on.

One may then ask how many components make it up, that is, how many faces, vertices, edges and cubes (its analog of the 3-d faces) can be counted in it? For that matter, given an n^th dimensional cube, how many components is it made up of?

In order to answer this let us first devise a suitable notation.

Let us designate a component by H, with the superscript indicating which component we are dealing with, and the subscript indicating in which dimension. The integer value of Hⁱ_j then indicates the i^th component in j^th space.

So a vertex (point) in a 1-dimensional space will be H⁰₀, whereas, for example, a cube will contain H⁰₃ vertices. The number of edges (i.e. lines) for a given polygon in n^th-dimensional space will be H¹_n, a face will be H²_n, a cube H³_n and so on. Obviously this will allow us to indicate as many dimensions as necessary, a 7^th-dimensional hyper-cube will contain H⁷₇, H⁶₇, H⁵₇ 1/4H⁰₇ components.

Let me introduce a recursive formula which will specify how many of a given component there are:

Given H⁰₀ = 1, we will define H^-1_n = 0   "n, thus giving the end values for the recursive formula. We should note that H may only assume non-negative values, for m £ n, otherwise it will be considered zero.²

Let us build up some concrete examples

For 0-dimensions we only have a point, and we have formally only one vertex, the point itself:

Given a line, we may consider a segment the 1-dimensional analog to the 2-dimensional square, and the formula gives us, the number of vertices:

and the number of edges (H¹):

At this point we assert that, Hⁿ_n = 1. The proof is by induction, since H⁰₀ = 1, assuming it true for any particular n it follows that it is true for n+1.

That this should be so is intuitively clear, since it is the n^th dimensional figure itself in n space that is being counted once.

It is also trivially true that H⁰_n = 2 ·H⁰_n-1. Again, it stands to reason, geometrically, that the number of vertices doubles as we ``drag'' an n-dimensional figure to create the (n+1)^th-dimensional one.

That H¹_n = 2 ·H¹_n-1 + H⁰_n-1 also stands to reason, since the number of edges will be twice that of the figure in (n-1)-space (its initial and final positions) plus the new edges created by the vertices being ``dragged''through n-space.

and for the edges:

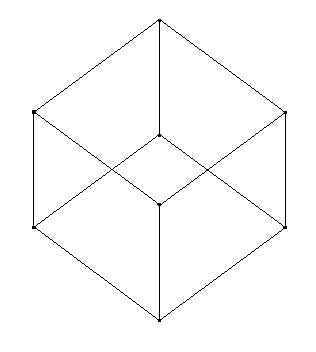
and number of faces:

Continuing some of the generalizations we get the following closed formulas,

we also have

as well as:

Carrying on some further generalizations we get the following closed formulas:

For H³_n we proceed along the same lines as above, it is just a bit more tedious.

These may be proved by induction.

To summarize the closed formulae,

It may be interesting to see these in Euler's formula, but modifying it somewhat,³ applied to a cube (or rectangular prism):

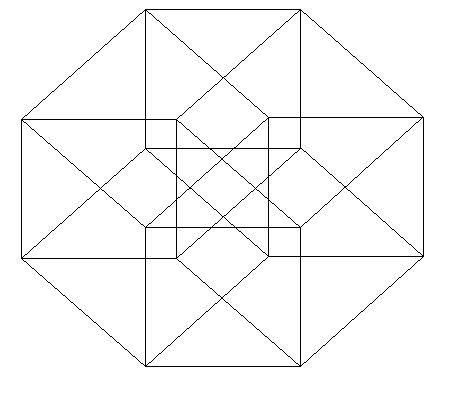
number of faces that make up a hyper-cube:

and number of 3d components or cubes:

again applying the (analog) of Euler's formula:

What is more interesting, generalizing Euler's formula using this notation we get:

we have, for the first few spaces Eⁿ

1. E⁰     H⁰₀ = 1
2. E¹     H⁰₁ - H¹₁ = 1
3. E²     H⁰₂ - H¹₂ + H²₂ = 1
4. E³     H⁰₃ - H¹₃ + H²₃ - H³₃ = 1
5. E⁴     H⁰₄ - H¹₄ + H²₄ - H³₄ + H⁴₄ = 1

For E⁰ and E¹ the formulae are trivially true, and it is quite easy to show it for E² as well.⁴ In E³ it is a trivial extension of Euler's formula, so that this is also true for all polygons.

The 4^th dimensional analog of the tetrahedron, the smallest regular solid in E₄ has 5 vertices, 10 edges, 10 faces and 5 (3-d) tetrahedrons. We can see that it too satisfies the general formula.

In E⁴ the proof for all hypercubes follows along the line of a proof for Euler's formula (at least as given in Courant's ``What is Mathematics?''), (Hⁿ_n - 1) - (H^n-1_n - 1) + 1/4( H⁰_n) = 1 leaves the value unvaried since the signs always alternate. We can continue the reasoning with the remaining components until we have reduced it to the identity 1 = 1 and this can be extended to E¹ for any n hypercubes.

Now it remains to be proved for figures other than hyper-cubes, and the inevitable conjecture is that

for any n-dimensional space, for any simple convex polytope:

n å i = 0  (-1)i ·Hin = 1

(2)

Footnotes:

¹ typeset by L^AT_EX

² That is, for m ³ n Þ H^m_n = 0.

³ The modification is to include the 3-d figure itself, denoted by ``C''. The reason why the formula has been modified will become clear shortly.

⁴ Every plane polygon (including concave polygons) has one side for each vertex, and thus H⁰₂ = H¹₂.

Last Update: February 6, 1999