Concorso europeo Philips per giovani inventori e ricercatori
Edizione 1982/83

Ero rimasto affascinato dalla proprietà delle funzioni esponenziali e trigonometriche di essere periodiche rispetto alla derivazione: la derivata di è ancora , se si deriva quattro volte consecutivamente una funzione circolare come seno o coseno, si ritorna alla stessa funzione.

Nonostante questa proprietà sia alla base di moltissime altre caratteristiche di queste funzioni, non vi è traccia in letteratura di alcun tentativo di generalizzare l’argomento definendo funzioni che derivate un numero arbitrario di volte ritornassero al punto di partenza.

Chiamai questa proprietà derivoperiodicità e conseguentemente mi proposi di costruire dette funzioni. L'idea iniziale, concepita intorno al '74, derivava da una semplice osservazione riguardante le serie di Taylor. Per l'esponenziale e per il coseno infatti vale:

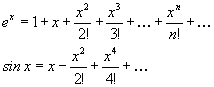
In pratica tutti i termini della serie sono del tipo e la derivata di questo termine è semplicemente cioè è ancora un termine della forma contenuta nelle serie. Lo sviluppo dell’esponenziale contiene tutti i termini, quindi quando si deriva la serie il termine successivo semplicemente diviene quello precedente, come se scorresse a sinistra.

Nella serie del seno, mancano i termini dispari e quelli pari sono a segni alterni. Quindi derivando una prima volta i termini pari divengono termini dispari. Derivando una seconda volta i termini dispari divengono pari, ma cambiati di segno. Derivando la terza volta i termini pari ridivengono dispari ma col segno cambiato. Derivando la quarta volta i termini dispari con il segno cambiato divengono pari ed il segno ricambia: si ritorna dunque alla prima serie, quella del seno.

La mia semplice osservazione fu che per creare una funzione derivoperiodica di ordine 3, cioè che ritornasse uguale dopo tre derivazioni, occorreva semplicemente creare una serie che avesse uno dei termini ogni tre

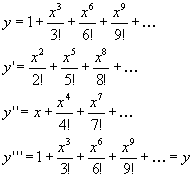
e questo era un meccanismo generalizzabile, quindi avrei potuto scrivere l’espressione in serie di una funzione derivoperiodica qualunque, con periodicità 5, 10 o 32.

Successivamente sviluppai la teoria e mi resi conto che l’espressione generale di una derivoperiodica può essere sempre descritta come somma di esponenziali con esponenti complessi.

Trovai una serie di interessanti proprietà, tra cui periodicità nel piano complesso, equazioni differenziali di cui dette funzioni sono soluzione, funzioni corrispondenti alla tangente e cotangente costruite sulle derivoperiodiche corrispondenti ecc.

In realtà la teoria presentata al concorso era solo un primo sviluppo. Chissà se riuscirò a sviluppare ulteriormente la teoria. Forse quando andrò in pensione…