Now we want to derive the field equations and the conservation laws of a classical field theory from an action principle. It will be clear in the treatment of the Noether theorem given in Section 4.3 that, if the conserved quantities are given by integrals of differential 3-forms on 3-dimensional surfaces, the action must be given by an integral of a differential 4-form on a 4-dimensional surface. This important idea has been proposed independently in refs. [3,4] and [51,52].
Note the difference with respect to the Kaluza-Klein theory [47,48] and its generalizations in a ![]() -dimensional space, in which the action is given by a
-dimensional space, in which the action is given by a ![]() -dimensional integral. We shall follow, with some simplifications, the treastment of refs. [3,5].
-dimensional integral. We shall follow, with some simplifications, the treastment of refs. [3,5].
It is convenient to use as dynamical variables the 1-forms
![]() and the scalar fields
and the scalar fields ![]() , where
, where ![]() is not necessarily a spinor index. Some of the fields
is not necessarily a spinor index. Some of the fields ![]() may be anticommuting quantities, that, after quantization, become Fermionic fields. Then, the order of some factors is relevant and we define the derivative of a function
may be anticommuting quantities, that, after quantization, become Fermionic fields. Then, the order of some factors is relevant and we define the derivative of a function ![]() with respect to the
quantity
with respect to the
quantity ![]() in such a way that
in such a way that
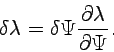 |
(4.14) |
If we exclude the presence of higher derivatives, the action principle takes the general form
| (4.16) |
We assume first that the variations ![]() and
and
![]() vanish on the surface
vanish on the surface ![]() , namely we put
, namely we put
| (4.18) |
| (4.19) |
The last equality can also be written in the form
| (4.20) |
| (4.21) |
The action principle takes the form
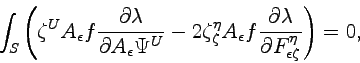 |
(4.22) |
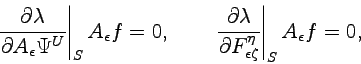 |
(4.23) |
Given five different indices
![]() , we can choose
, we can choose ![]() and
and ![]() in such a way that, at a given point of
in such a way that, at a given point of ![]() , only the restrictions of
, only the restrictions of
![]() do not vanish and only
do not vanish and only
![]() is not zero. In this way we obtain the conditions
is not zero. In this way we obtain the conditions
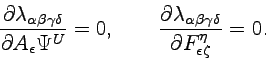 |
(4.24) |
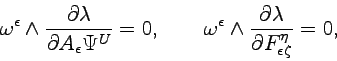 |
(4.25) |
Since these condition hold for any choice of the basis in the space ![]() , for any choice of the coefficients
, for any choice of the coefficients
![]() we have
we have
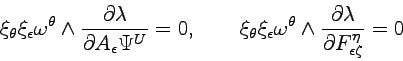 |
(4.26) |
If we apply the interior product operator
![]() to these equations, we obtain
to these equations, we obtain
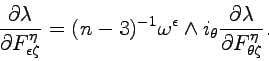 |
(4.30) |
Now we simplify the action principle by means of the equations (4.29), (4.31) and we derive another set of field equations called the tangential field equations. We consider a general choice of ![]() and
and
![]() and we have
and we have
By means of the generalized Stokes theorem, we obtain
| (4.37) |