Contents

• • Introduction
  • Notations and conventions
  • Some useful identities
  
  
• The (extended) principal fiber bundle of the Lorentz frames
  • Tetrads
  • Tensor and spinor fields
  • Infinitesimal Lorentz transformations
  • Maxwell and Yang-Mills fields
  • Parallel transport
  • Covariant derivatives and spin connection
  • A compact formalism
  • Connection, soldering, curvature and torsion forms
  • Flat Minkowski spacetime and Poincaré group
  
  
• The general space $\mathcal{S}$ of the (extended) inertial local frames
  • The basic geometric and topological stucture of the space $\mathcal{S}$
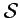
  • The operational interpretation and the relativity principle
  • The spacetime coincidence
  • The equity principle, the minimum time principle and the fundamental length
  • Dynamical variables and symmetry properties
  • Critical remarks
  
  
• Feasibility of infinitesimal transformations and geometric symmetry groups
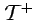  • A wedge $\mathcal{T}^+$ in the vector space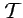 $\mathcal{T}$
  • The Lorentz invariant cone $\mathcal{T}^+$
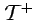
  • The symmetry group $GL(4, \mathbf{R})$
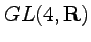
  • Orbits in 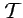$\mathcal{T}$ and causal influence
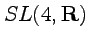  • $SL(4, \mathbf{R})$ spinors and 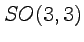$SO(3,3)$ tensors
  • Subgroups of $SL(4, \mathbf{R})$
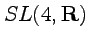
  • The spinor representation of the structure coefficients
  • Subgroups of 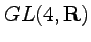$GL(4, \mathbf{R})$ as gauge groups?
  
  
• Lagrangian dynamics of classical fields
  • Conserved forms
  • The action principle and the field equations
  • Noether's theorem
  • Minimal coupling and the balance equations
  • Pre-symplectic formalism and double differential forms
  
  
• Reformulation of some classical field theories
  • The Einstein-Cartan theory of gravitation
  • Internal gauge theories
  • Scalar fields
  • Spinor fields
  • Fermions in the Standard Model of elementary particles
  
  
• Theories with a variable gravitational coupling
  • A geometrized scalar-tensor theory of gravitation
  • Macroscopic physical interpretation
  • Microscopic considerations and dilatations of $\mathcal{T}$.
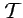  • Lagrangian constraints and pre-symplectic double forms
  
  
• Classical field theories with $Sp(4, \mathbf{R})$ symmetry (not complete)
  • Higher symmetries and a substitution rule
  • Normal field equations and use of the symmetry property.
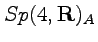  • Two examples of Lagrangians invariant under $Sp(4, \mathbf{R})_A$.
  
  
• Test particles in geometric fields (not ready)
• Cosmological applications (not ready)
• Graded field algebras and antiderivations (not ready)
• Quantum fields in a fixed geometric background (not ready)
• Bibliography
• Index