Maxwell and Yang-Mills fields

As the theories of gravitation, also the gauge field theories with internal gauge group $\mathcal{G}$ [41] have an elegant geometric treatment in the framework of a principal fibre bundle with structural group $\mathcal{G}$ [42]. We always specify ``internal'' because gravitation too is described by a gauge theory. If $\mathcal{G} = U(1) = SO(2)$, we obtain Maxwell's electromagnetism and for $\mathcal{G} = SU(2)$ we have the original Yang-Mills theory [43].

Several authors [44,45,46] have proposed a unified treatment of gravitation and internal gauge theories based on a principal fibre bundle with base $\mathcal{M}$ and structural group $\mathcal{L} \times \mathcal{G}$. If $\mathcal{G}$ is a Lie group with dimension $n$, this bundle has dimension $10 + n$. We call it the bundle of extended frames and we indicate it by $\mathcal{S}_n$. It can also be considered as a principal fibre bundle with base $\mathcal{S}$ and structural group $\mathcal{G}$. Of course, if $n = 0$ we have $\mathcal{S}_0 = \mathcal{S}$. This approach is similar to the Kaluza-Klein unification of gravitation and electromagnetism [47,48], but it is conceptually rather different.

The right action of $\mathcal{G}$ on $\mathcal{S}_n$ is generated by $n$ vector fields $A_a$, where the index $a$ labels a basis of the Lie algebra of $\mathcal{G}$. In the treatment of the Maxwell field, we have $n = 1$ and we indicate the generator of the electromagnetic gauge transformations by $A_{\bullet}$. If $n > 1$, the vector fields $A_a$ satisfy the commutation relations (or Lie brackets)

$$[A_{[ik]}, A_a] = 0, \qquad [A_a, A_b] = \hat F_{ab}^c A_c,$$ (1.19)

where $\hat F_{ab}^c$ are the structure constants of the Lie algebra of $\mathcal{G}$.

In order to obtain a local parametrization of $\mathcal{S}_n$, we have to choose, besides a local coordinate system in $\mathcal{M}$, a gauge at every point $x \in \mathcal{M}$. Then the extended frame $s \in \mathcal{S}_n$ is determined by the quantities $(x^{\mu}, e^{\mu}_i, g)$, where $g \in \mathcal{G}$, represents the gauge transformation from the conventionally chosen gauge at $x = \pi(s)$ to the gauge choice at $s$. The group element $g$, in turn, can be locally parametrized by $n$ real coordinates. Note that $g$ is not affected by the right action of the Lorentz group $\mathcal{L}$. The generators $A_a$ of the internal gauge transformations also describe the infinitesimal right translations of the group $\mathcal{G}$ and there is no problem in using the same symbols for the vector fields defined in $\mathcal{S}_n$ and in $\mathcal{G}$.

In Section 1.5 we need the vector fields $A^L_a$ that generate the left translations on the group $\mathcal{G}$. They commute with the generators $A_a$ of the right translations and satisfy the commutation relations

$$[A^L_a, A^L_b]= - \hat F_{ab}^c A^L_c$$ (1.20)

(note the minus sign). They can be written in the form

$$L^L_a = D^b{}_a(g^{-1}) A_b,$$ (1.21)

where the matrices $D^b{}_a$ belong to the adjoint representation of $\mathcal{G}$. The vector fields $A^L_a$, originally defined on $\mathcal{G}$, can also be considered as vector fields on $\mathcal{S}_n$, but in this case they depend on the choice of the parametrization.

In Section 1.8 we use the left invariant Maurer-Cartan one-forms $\chi^b$ on the gauge group $\mathcal{G}$ defined by the formula

$$\chi^b(A_a) = \delta_a^b.$$ (1.22)

They can be written in terms of the local coordinates of the group $\mathcal{G}$ and they can also be considered as differential forms defined on $\mathcal{S}_n$, which, however depend on the choice of the parametrization. In any case we have [25,26]

$$d \chi^{a} = - 2^{-1} \hat F_{b c}^a \, \chi^b \wedge \chi^c.$$ (1.23)

The group $\mathcal{G}$ acts linearly on the fields. If, as in eq. (1.14), we consider the field components as the elements of a one-column matrix $\Psi$, we have

$$\Psi(sg) = \Sigma(g^{-1}) \Psi$$ (1.24)

and the infinitesimal transformations are given by

$$A_a \Psi = - \Sigma_a \Psi.$$ (1.25)

The matrices $\Sigma_a$ form a representation of the Lie algebra of $\mathcal{G}$, namely

$$[\Sigma_a, \Sigma_b]= \hat F_{ab}^c \Sigma_c .$$ (1.26)

We use the same symbol $\Sigma$ for both the representations of $\mathcal{L}$ and of $\mathcal{G}$, because we consider them as special cases of a representation of the structural group $\mathcal{L} \times \mathcal{G}$.

If $\mathcal{G} = U(1)$, $g$ is a phase factor and it is convenient to put $g = \exp(ie \varphi)$, where $\varphi$ is a cyclic real parameter with period $2 \pi e^{-1}$ and $e$ is the elementary electric charge. In this case we have

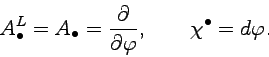$$A^L_{\bullet} = A_{\bullet} = \frac{\partial}{\partial \varphi}, \qquad \chi^{\bullet} = d \varphi.$$ (1.27)

If $\Psi$ is a complex field carrying the electric charge $Ze$, we have

$$A_{\bullet} \Psi = \frac{\partial}{\partial \varphi} \Psi = - \Sigma_{\bullet} \Psi = - i Z e \Psi.$$ (1.28)