The Lorentz invariant cone
Assuming ![]() , namely disregarding the internal gauge transformations, if we want to satisfy the equity and the minimum time principles (see Section 2.4), a nonvanishing element of
, namely disregarding the internal gauge transformations, if we want to satisfy the equity and the minimum time principles (see Section 2.4), a nonvanishing element of ![]() must have
must have ![]() , since all the physical operations ``take some time''. It follows that
, since all the physical operations ``take some time''. It follows that ![]() is a closed cone with a nonempty interior and we call it the feasibility cone. We say that a theory of this kind has a modified geometry. In the presentation of this argument we follow refs. [7,11,14].
is a closed cone with a nonempty interior and we call it the feasibility cone. We say that a theory of this kind has a modified geometry. In the presentation of this argument we follow refs. [7,11,14].
In order to determine the structure of ![]() , we have to assume some symmetry property and a natural requirement is that, as in the normal theories, it is symmetric under the proper orthochronous Lorentz group
, we have to assume some symmetry property and a natural requirement is that, as in the normal theories, it is symmetric under the proper orthochronous Lorentz group
![]() . More precisely, we write an element of
. More precisely, we write an element of ![]() in the form (3.3) and we require the invariance under the Lorentz transformations
in the form (3.3) and we require the invariance under the Lorentz transformations
If ![]() contains an element with coordinates
contains an element with coordinates
![]() , it contains also the element with co-ordinates
, it contains also the element with co-ordinates
![]() , which belongs to the convex hull of a finite set of points obtained from the given point by means of suitable rotations. The dilatation invariant set of the possible values of
, which belongs to the convex hull of a finite set of points obtained from the given point by means of suitable rotations. The dilatation invariant set of the possible values of ![]() cannot be reduced to
cannot be reduced to ![]() , because
, because ![]() generates
generates ![]() and cannot be the whole real line because
and cannot be the whole real line because ![]() is a cone. It follows that it is the half line
is a cone. It follows that it is the half line ![]() or the half line
or the half line ![]() . For physical reasons, we choose the second possibility. In order to avoid that, after a Lorentz transformation,
. For physical reasons, we choose the second possibility. In order to avoid that, after a Lorentz transformation, ![]() becomes negative, we have to assume that
becomes negative, we have to assume that ![]() is contained in the wedge defined by eq. (3.5).
is contained in the wedge defined by eq. (3.5).
We consider an arbitrary element of the interior of ![]() and we simplify its coordinates by means of a suitable Lorentz transformation. Since the four-vector
and we simplify its coordinates by means of a suitable Lorentz transformation. Since the four-vector ![]() is timelike, we can obtain
is timelike, we can obtain
![]() . Then, by means of a rotation, we can cancel the third components of
. Then, by means of a rotation, we can cancel the third components of ![]() and
and ![]() . In conclusion, we obtain
. In conclusion, we obtain
| (3.8) |
We indicate by
![]() the coordinates obtained from
the coordinates obtained from ![]() by means of a Lorentz boost with rapidity
by means of a Lorentz boost with rapidity ![]() along the third space axis
and we define the quantities
along the third space axis
and we define the quantities
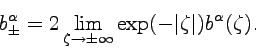 |
(3.9) |
![$\textstyle b^0_{\pm} = b^0, \quad
b^{[01]}_{\pm} = b^{[01]} \pm b^{[31]}, \quad
b^{[32]}_{\pm} = b^{[32]} \pm b^{[02]},$](img444.png) |
|||
![$\textstyle b^3_{\pm} = \pm b^0, \quad
b^{[02]}_{\pm} = b^{[02]} \pm b^{[32]}, \quad
b^{[13]}_{\pm} = b^{[13]} \pm b^{[10]}$](img445.png) |
(3.10) |
| (3.11) |
We have shown that the element considered is the sum of two elements of ![]() that satisfy the conditions
that satisfy the conditions
| (3.13) |
One can easily see that ![]() acts transitively on the sets
acts transitively on the sets ![]() , which are either contained in
, which are either contained in ![]() or do not intersect it. The first possibility is realized if
or do not intersect it. The first possibility is realized if ![]() belongs to a closed convex set containing the point
belongs to a closed convex set containing the point ![]() and bounded, otherwise for fixed
and bounded, otherwise for fixed ![]() arbitrarily large values of
arbitrarily large values of ![]() and
and ![]() would be permitted and
would be permitted and ![]() would not be a cone. In other words, we must have
would not be a cone. In other words, we must have
![]() , where
, where ![]() is a positive fundamental length. One can easily see that if this inequality is satisfied, every element of
is a positive fundamental length. One can easily see that if this inequality is satisfied, every element of ![]() can be written as the sum of two elements of
can be written as the sum of two elements of
![]() .
.
In conclusion, we have proven that all the elements of the interior of ![]() can be written as the sum of two elements of
can be written as the sum of two elements of ![]() with
with ![]() or of four elements of
or of four elements of
![]() . Since
. Since ![]() is the closure of its interior, it is easy to show that all its elements have the same decomposition. Note that, if
is the closure of its interior, it is easy to show that all its elements have the same decomposition. Note that, if
![]() ,
,
![]() ,
,
![]() and
and
![]() form a left-handed triad of normalized orthogonal vectors.
form a left-handed triad of normalized orthogonal vectors.
From the decomposition of an element of ![]() into elements of
into elements of
![]() and eq. (3.12), we obtain immediately the inequalities
and eq. (3.12), we obtain immediately the inequalities
| (3.14) |