A wedge
In Section 2.2 we have introduced the n-dimensional vector space ![]() generated by its subset
generated by its subset
![]() which contains all the vector fields that describe feasible infinitesimal transformations, namely semigroups of operationally defined transformations. Note that not all the elements of
which contains all the vector fields that describe feasible infinitesimal transformations, namely semigroups of operationally defined transformations. Note that not all the elements of ![]() belong to
belong to ![]() . For instance, the vector field
. For instance, the vector field ![]() generates time translations in the past, which cannot be realized. In other terms, one cannot build a situation (local frame) in the past. The properties of
generates time translations in the past, which cannot be realized. In other terms, one cannot build a situation (local frame) in the past. The properties of ![]() have been discussed in refs. [7,11,12,14].
have been discussed in refs. [7,11,12,14].
It is clear that ![]() is dilatation invariant and we also assume that it is closed. If
is dilatation invariant and we also assume that it is closed. If
![]() , we have [84]
, we have [84]
| (3.1) |
A cone is a wedge that does not contain straight lines. If ![]() is not a cone, the linear subspace
is not a cone, the linear subspace
![]() , that contains the reversible infinitesimal transformations, has positive dimension. We consider two vector fields
, that contains the reversible infinitesimal transformations, has positive dimension. We consider two vector fields ![]() belonging to this subspace. Since
belonging to this subspace. Since
![]() , from the formula [84]
, from the formula [84]
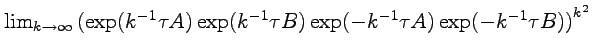 |
|||
| (3.2) |
It is convenient to write a generic vector of ![]() in the form
in the form
In the normal theories all the Lorentz transformation and the spacetime translations belonging to the closed future cone are feasible, namely ![]() is a wedge defined by the inequality
is a wedge defined by the inequality
| (3.6) |
One may say that in a normal theory it takes some time to perform a space translation, but it takes no time to perform a rotation or a Lorentz boost. Of course, it takes no time to perform internal gauge transformations.