- Tetrads
- Tensor and spinor fields
- Infinitesimal Lorentz transformations
- Maxwell and Yang-Mills fields
- Parallel transport
- Covariant derivatives and spin connection
- A compact formalism
- Connection, soldering, curvature and torsion forms
- Flat Minkowski spacetime and Poincaré group
- The basic geometric and topological stucture of the space
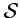
- The operational interpretation and the relativity principle
- The spacetime coincidence
- The equity principle, the minimum time principle and the fundamental length
- Dynamical variables and symmetry properties
- Critical remarks
- A wedge
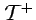 in the vector space
in the vector space 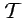
- The Lorentz invariant cone
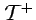
- The symmetry group
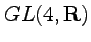
- Orbits in
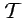 and causal influence
and causal influence
-
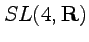 spinors and
spinors and 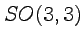 tensors
tensors
- Subgroups of
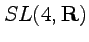
- The spinor representation of the structure coefficients
- Subgroups of
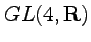 as gauge groups?
as gauge groups?
- Conserved forms
- The action principle and the field equations
- Noether's theorem
- Minimal coupling and the balance equations
- Pre-symplectic formalism and double differential forms
- The Einstein-Cartan theory of gravitation
- Internal gauge theories
- Scalar fields
- Spinor fields
- Fermions in the Standard Model of elementary particles
- A geometrized scalar-tensor theory of gravitation
- Macroscopic physical interpretation
- Microscopic considerations and dilatations of
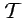 .
.
- Lagrangian constraints and pre-symplectic double forms
- Higher symmetries and a substitution rule
- Normal field equations and use of the symmetry property.
- Two examples of Lagrangians invariant under
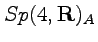 .
.