Normal field equations and use of the symmetry property.

The Lagrangians studied in Chapter 5 have a particular structure that permits a simpler treatment of the normal field equations. In the present Chapter too, we consider Lagrangian of the form

$$\lambda = d \omega^{\alpha} \wedge \sigma_{\alpha} + \lambda^A + \lambda^M,$$ (7.17)

where the quantities $\sigma_{\alpha}$, $\lambda^A$, and $\lambda^M$ contain, besides the forms $\omega^{\alpha}$, the field $\phi$ defined by eq. (7.5) and the fields

$$\chi_{\alpha} = F_{\alpha \beta}^{\beta}, \qquad \chi_i = F... ...quad \chi_{[ik]} = F_{[ik]j}^j + 2^{-1} F_{[ik][jl]}^{[jl]}.$$ (7.18)

Note that these fields are not exactly equal to the fields indicated by the same symbols in eqs. (6.1) and (6.2). They have similar properties, but transform in a simpler way. After the application of the substitution rule, also the fields $\psi_u$ appear in the Lagrangian. Instead of the fields $\phi$ and $\psi_u$, one can use directly the fields $f_u$.

The derivatives of $\lambda$ with respect to the structure coefficients that appear in the normal field equation (4.28) contain two contributions, one coming from the exterior derivatives $d \omega^{\alpha}$ and the other originated by the dependence of $\lambda$ on the quantities $f_u$ and $\chi_{\alpha}$. The first contribution satisfies the normal field equations automatically and the second contribution gives the condition

$$\left( \frac{\partial f_u}{\partial F_{\epsilon \zeta}^{\eta... ...) \wedge \frac{\partial \lambda}{\partial \chi_{\alpha}} = 0,$$ (7.19)

or, more explicitly, by using the 5-dimensional tensor notation and eqs. (3.93) and (7.18),

$$\alpha \left((\delta_u^v \epsilon_{yy'}{}^{v'ww'} - \delta_u^{v'} \e... ...{yy'}{}^{w'vv'} + \delta_u^{w'} \epsilon_{yy'}{}^{wvv'}) \omega^{[xx'5]}\right.$$

$$\left. + (\delta_u^x \epsilon_{yy'}{}^{x'ww'} - \delta_u^{x'} \epsil... ...{}^{wxx'}) \omega^{[vv'5]} \right) \wedge \frac{\partial \lambda}{\partial f_u}$$

$$+ \beta \left((\delta_{uu'}^{vv'} \delta_{yy'}^{ww'} - \delta_{uu'}^{ww'} \delta_{yy'}^{vv'}) \omega^{[xx'5]}\right.$$

$$\left. + (\delta_{uu'}^{xx'} \delta_{yy'}^{ww'} - \delta_{uu'}^{ww'}... ...ga^{[vv'5]} \right) \wedge \frac{\partial \lambda}{\partial \chi_{[uu'5]}} = 0,$$ (7.20)

where $\alpha$ and $\beta$ are irrelevant constant coefficients and

$$\delta_{uu'}^{vv'} = \delta_u^v \delta_{u'}^{v'} - \delta_{u'}^v \delta_u^{v'}.$$ (7.21)

We fix arbitrarily the indices $u = v = y$ and $x \neq x'$, and without loss of generality we assume, for instance, that $u \neq x$. Then we chose $y' \neq y, x, x'$ and $v' \neq v, x, x', y'$. We choose the other indices $w, w'$ in such a way that $y, y', v', w, w'$ are all different. Then only the first term of eq. (7.20) survives and we have

$$\omega^{[xx'5]} \wedge \frac{\partial \lambda}{\partial f_u} = 0.$$ (7.22)

By reasoning as in the case of eq. (6.8) we obtain

$$\frac{\partial \lambda}{\partial f_u} = 0.$$ (7.23)

In order to treat the second part of eq. (7.19), we write it in the form

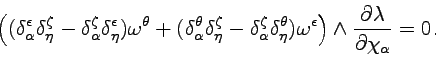$$\left( (\delta_{\alpha}^{\epsilon} \delta_{\eta}^{\zeta} - \... ...) \wedge \frac{\partial \lambda}{\partial \chi_{\alpha}} = 0.$$ (7.24)

We choose arbitrarily the indices $\alpha = \zeta$ and $\theta$. It is always possible to put $\epsilon = \eta \neq \alpha, \theta$ and we obtain

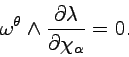$$\omega^{\theta} \wedge \frac{\partial \lambda}{\partial \chi_{\alpha}} = 0.$$ (7.25)

It follows that

$$\frac{\partial \lambda}{\partial \chi_{\alpha}} = 0.$$ (7.26)

For the particular kind of Lagrangians we are considering, eqs. (7.23) and (7.26) are equivalent to the normal equation (4.28). By introducing the variables $\phi, \psi_i$, eq (7.23) can also be written in the form

$$\frac{\partial \lambda}{\partial \psi_i} = 0$$ (7.27)

$$\frac{\partial \lambda}{\partial \phi} = 0.$$ (7.28)

From eq. (7.17) and the normal field equations (7.23) and (7.26) we have

$$\frac{\partial \lambda}{\partial F_{\alpha \beta}^{\gamma}} ... ...} \omega^{\alpha} \wedge \omega^{\beta} \wedge \sigma_{\gamma}$$ (7.29)

in agreement with eq. (4.31). The subscript $E$ means that the partial derivative takes into account only the explicit dependence of $\lambda$ on the structure coefficients and not the indirect dependence through the quantities $f_u$ and $\chi_{\alpha}$.

The conservation laws corresponding to the infinitesimal $Sp(4, \mathbf{R})_A$ symmetry transformations play an important role in the following discussion. As it is explained in Section 4.5, these transformations are generated by the vector fields $X_{[uv]}$ (in the phase space) that act on the dynamical variables in the following way

$$X_{[uv]} \omega^{[xy5]} = \delta^x_u g_{vz} \omega^{[zy5]} + \delta^... ...^{[xz5]} - \delta^x_v g_{uz} \omega^{[zy5]} - \delta^y_v g_{uz} \omega^{[xz5]},$$

$$X_{[uv]} \phi = 0, \qquad X_{[uv]} \psi_w = g_{uw} \psi_v - g_{vw} \psi_u,$$

$$X_{[uv]} \chi_{[xy5]} = g_{xu} \delta_v^z \chi_{[zy5]} + g_{yu} \del... ...\chi_{[xz5]} - g_{xv} \delta_u^z \chi_{[zy5]} - g_{yv} \delta_u^z \chi_{[xz5]}.$$ (7.30)

According to eq. (4.41), this symmetry gives rise to the conservation laws

$$d \theta_{[uv]} = 0, \qquad \theta_{[uv]} = \theta^G_{[uv]} + \theta^M_{[uv]},$$ (7.31)

where

$$\theta^G_{[uv]} = X_{[uv]}\omega^{\alpha} \wedge \sigma_{\alpha}, \qquad \theta^M_{[uv]} = X_{[uv]} \Psi^U \pi_U.$$ (7.32)

These conservation laws, are a consequence of all the field equations and we want to show that, when all the other field equations are satisfied, the normal equation (7.27) is equivalent to the following equation that sometimes has an easier treatment and a more direct meaning:

$$\psi^u d \theta_{[uv]} = 0.$$ (7.33)

We use the invariance property of $\lambda$, which, using the shorthand notation introduced in Section 7.1, can be written in the form

$$X_{[uv]} \lambda = X_{[uv]} Z \frac{\partial \lambda}{\parti... ...+ X_{[uv]} \psi_w \frac{\partial \lambda}{\partial \psi_w}= 0,$$ (7.34)

or, more explicitly,

$$X_{[uv]} \Psi^U \frac{\partial \lambda}{\partial \Psi^U} + X_{[uv]} (A_{\alpha} \Psi^U) \frac{\partial \lambda}{\partial A_{\alpha} \Psi^U}$$

$$- 2^{-1} X_{[uv]} F_{\alpha \beta}^{\gamma} \omega^{\alpha} \wedge \... ...\alpha} \lambda + X_{[uv]} \psi_w \frac{\partial \lambda}{\partial \psi_w} = 0,$$ (7.35)

where eqs. (7.26) and (7.29) have been taken into account.

By means of the normal field equation (4.29) and of the tangential equations (4.34), (4.35) and (4.36), we obtain

$$d (X_{[uv]} \Psi^U \pi_U) - A_{\alpha} \Psi^U (X_{[uv]} \omega^{\alpha}) \wedge \pi_U + d (X_{[uv]} \omega^{\alpha}) \wedge \sigma_{\alpha}$$

$$+ F_{\alpha \beta}^{\gamma} X_{[uv]} \omega^{\alpha} \wedge \omega^{... ...} i_{\alpha} \lambda + X_{[uv]} \psi_w \frac{\partial \lambda}{\partial \psi_w}$$

$$= d (X_{[uv]} \Psi^U \pi_U) - (X_{[uv]} \omega^{\alpha}) \wedge \tau_{\alpha}$$

$$+ d (X_{[uv]} \omega^{\alpha}) \wedge \sigma_{\alpha} + X_{[uv]} \psi_w \frac{\partial \lambda}{\partial \psi_w} = 0$$ (7.36)

and finally

$$d \theta_{[uv]} + (g_{uw} \psi_v - g_{vw} \psi_u) \frac{\partial \lambda}{\partial \psi_w} = 0.$$ (7.37)

If the normal equation (7.27) is satisfied (as well as all the other field equations) this is just a new proof of the conservation of $\theta_{[uv]}$. Conversely, if we assume eq. (7.33), we easily obtain the normal equation (7.27), as we have anticipated above.

In the analysis of the field equations, a considerable simplification can be obtained by choosing an adapted basis in the space $\mathcal{T}$ by means of a suitable (global) transformation of the symmetry group $Sp(4, \mathbf{R})_A$. In this way, assuming the inequality (7.8), we can put, at a single distinguished point $\hat s \in \mathcal{S}$, $f_i = 0$ or $\psi_i = 0$. At this point the Lagrangian form $\lambda$ is not affected by the substitution rule. Besides $\lambda$, also $\pi$, $\sigma_{\alpha}$, $\theta_{[uv]}$, and $\tau_{\alpha}$ have, at the particular point $\hat s$, the same form they have before the application of the substitution rule. In particular, the quantities $\tau^M_{\alpha}$ have the local form (4.68).

However, one has to be careful in dealing with expressions containing derivatives with respect to $\psi_i$ or other differential operators applied to expressions containing $\psi_i$: one has to compute the derivatives first and then to put $\psi_i = 0$. For instance, the field equations and the conservation laws may contain new terms that do not vanish at the point $\hat s$. In order to compute them, we need the derivatives of various quantities with respect to $\psi_i$ at the point $\hat s$.

In some simple cases, these derivatives can be obtained directly or by means of eq. (7.16). They can also be obtained by means of the covariance of these quantities with respect to the infinitesimal transformations $X{[j4]}$ given by

$$X_{[i4]} \Psi = \Sigma_{[i4]} \Psi,$$

$$X_{[i4]} \omega^j = - 2^{-1} \ell \epsilon^j{}_{ikl} \omega^{[kl]}, \qquad X_{[i4]} \omega^{[jk]} = - \ell^{-1} \epsilon^{jk}{}_{il} \omega^l,$$

$$X_{[i4]} \chi_j = - 2^{-1} \ell^{-1} \epsilon_{ji}{}^{kl} \chi_{[kl]} \qquad X_{[i4]} \chi_{[jk]} = - \ell \epsilon_{jki}{}^{l} \chi_l.$$ (7.38)

$$X_{[i4]} \pi = - \Sigma^T_{[i4]} \pi,$$

$$X_{[i4]} \sigma_j = - 2^{-1} \ell^{-1} \epsilon_{ji}{}^{kl} \sigma_{[kl]}, \qquad X_{[i4]} \sigma_{[jk]} = - \ell \epsilon_{jki}{}^l \sigma_l,$$

$$X_{[i4]} \theta_{[jk]} = g_{ik} \theta_{[j4]} - g_{ij} \theta_{[k4]}, \qquad X_{[i4]} \theta_{[j4]} = \theta_{[ji]}.$$ (7.39)

By using the shorthand notation introduced at the end of Section 7.1, since at the point $\hat s$ it is

$$X_{[i4]} \psi_k = g_{ik}\psi_4 = g_{ik}, \qquad X_{[i4]} \psi_4 = \psi_i = 0,$$ (7.40)

we obtain, at the same point,

$$\frac{\partial \pi}{\partial \psi^i} = - \Sigma^T_{[i4]} \pi - \frac{\partial \pi}{\partial Z} X_{[i4]} Z,$$

$$\frac{\partial \sigma_j}{\partial \psi^i} = - 2^{-1} \ell^{-1} \epsilon_{ji}{}^{kl} \sigma_{[kl]} - \frac{\partial \sigma_j}{\partial Z} X_{[i4]} Z,$$

$$\frac{\partial \sigma_{[jk]}}{\partial \psi^i} = - \ell \epsilon_{jki}{}^l \sigma_l - \frac{\partial \sigma_{[jk]}}{\partial Z} X_{[i4]} Z,$$

$$\frac{\partial \theta_{[jk]}}{\partial \psi^i} = g_{ik} \theta_{[j4]} - g_{ij} \theta_{[k4]} - \frac{\partial \theta_{[jk]}}{\partial Z} X_{[i4]} Z,$$

$$\frac{\partial \theta_{[j4]}}{\partial \psi^i} = \theta_{[ji]} - \frac{\partial \theta_{[j4]}}{\partial Z} X_{[i4]} Z.$$ (7.41)

In many situations the ``old'' theory, considered before the application of the substitution rule, agrees with a good accuracy with the empirical data. As a consequence, it is important to understand the conditions under which the solutions of the ``old'' theory are also solutions of the ``new'' theory obtained by means of the substitution rule. For these solutions we have 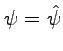$\psi = \hat \psi$ and the corrections to the field equations, proportional to derivatives of $\psi$ vanish. However, the ``new'' theory has the additional normal equation (7.27), equivalent to the conservation law (7.33), that in the case we are considering takes the form $d \theta_{[i4]} = 0$. If and only if it astisfies this equation a solution of the ``old'' theory is also a solution of the ``new'' theory.