In Section 2.5 we have introduced the geometric symmetry group of the field equations ![]() and in Section 3.3 we have suggested that it is a subgroup of the symmetry group
and in Section 3.3 we have suggested that it is a subgroup of the symmetry group
![]() of the cone
of the cone ![]() . In the present Chapter we deal with field theories with a geometric symmetry group
. In the present Chapter we deal with field theories with a geometric symmetry group ![]() larger than the Lorentz group. In this way we introduce the new fundamental constant
larger than the Lorentz group. In this way we introduce the new fundamental constant ![]() .
.
A detailed analysis of the possible geometric symmetry groups containing the Lorentz group was given in ref. [6]. Since at that time the explicit forms of the cone ![]() and of its symmetry group were not known, one had to consider all the sugroups of the group
and of its symmetry group were not known, one had to consider all the sugroups of the group
![]() containing all the linear transformations of
containing all the linear transformations of ![]() and a definite choice could not be obtained. In this analysis the most relevant group
and a definite choice could not be obtained. In this analysis the most relevant group
![]() was omitted and an erratum [6] was published to correct this mistake.
was omitted and an erratum [6] was published to correct this mistake.
The higher symmetry theories should not contradict the normal Lorentz symmetric theories treated in Chapter 5 in their range of validity. Einstein's General Relativity has been confirmed with high precision by laboratory experiments, for instance on the equivalence principle, and by accurate observations of the planetary system and of the binary pulsars. For an updated review, see ref. [109]. The Einstein-Cartan theory is not, at present, experimentally distinguishable from General Relativity and we prefer it in the present notes only because it gives a more symmetric treatment of energy-momentum and spin, in agreement with the equity principle (see Section 2.4). Also the Brans-Dicke scalar-tensor theory cannot be distinguished from General Relativity if the parameter ![]() is sufficently large.
is sufficently large.
There is some possibility for modifications of Einstein's gravitational theory at very small distances, or very large curvatures, and at very large distances, which appear in the galactic and cosmological observations. It may look strange that the phenomena at very large distance can be influenced by the introduction of a very small fundamental length. It is possible, however, that very small local effects due to the fundamental length accumulate over very long distances giving observable effects. This idea has been discussed, in a different context, in ref. [111].
In the search of new theories, it is important to take into account a ``correspondence principle'' that requires that the old theory is, in some way, a limit of the new theory. The simplest example is the nonrelativistic limit of a relativistic particle. If we consider the particle Lagrangians as differential 1-forms and we reintroduce the symbol ![]() for the velocity of light, we have
for the velocity of light, we have
| (7.1) |
| (7.2) |
| (7.3) |
We could expect a similar situation when we consider the normal limit ![]() of a theory with higher symmetry, but the Lagrangian forms of the normal theories examined in Chapter 5 are not quasi-invariant with respect to any of the contracted transformations given by eqs. (3.81) and (3.82). This remark could be discouraging, but we have to consider that our problem has some more complications. In particular, as we have remarked in Section 3.7, the higher symmetry group is spontaneously broken and there are several nonsymmetric vacuum states. It follows that it is not sufficient to consider the limit
of a theory with higher symmetry, but the Lagrangian forms of the normal theories examined in Chapter 5 are not quasi-invariant with respect to any of the contracted transformations given by eqs. (3.81) and (3.82). This remark could be discouraging, but we have to consider that our problem has some more complications. In particular, as we have remarked in Section 3.7, the higher symmetry group is spontaneously broken and there are several nonsymmetric vacuum states. It follows that it is not sufficient to consider the limit ![]() , but one has also to choose one of the degenerate vacuum states. The new Lagrangian should approach the old Lagrangian only for configurations which are, in some sense, near to one of the vacuum states, that becomes the unique vacuum state of the old theory. In this way the quasi-invariance of the old Lagrangian with respect to the contracted high-symmetry group is lost.
, but one has also to choose one of the degenerate vacuum states. The new Lagrangian should approach the old Lagrangian only for configurations which are, in some sense, near to one of the vacuum states, that becomes the unique vacuum state of the old theory. In this way the quasi-invariance of the old Lagrangian with respect to the contracted high-symmetry group is lost.
In order to obtain a gravitational Lagrangian form with higher symmetry by means of a minimal modification of a known Lorentz invariant Lagrangian form of the kind considered in Chapter 5, one can rewrite the latter by using the spinor formalism, namely introducing the forms ![]() and the structure coefficients
and the structure coefficients
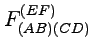 . The expression obtained in this way must also contain the antisymmetric constant Lorentz invariant spinors
. The expression obtained in this way must also contain the antisymmetric constant Lorentz invariant spinors ![]() and
and ![]() defined in Sections 3.3 and 3.5, that, however, are not invariant under
defined in Sections 3.3 and 3.5, that, however, are not invariant under
![]() . A Lagrangian symmetric under a larger group can be obtained by replacing these constant spinors by antisymmetric spinor expressions obtained from the structure coefficients by means of the rules of the spinor calculus. We call this procedure the substitution rule.
. A Lagrangian symmetric under a larger group can be obtained by replacing these constant spinors by antisymmetric spinor expressions obtained from the structure coefficients by means of the rules of the spinor calculus. We call this procedure the substitution rule.
Of course, the new expressions must be very near to the constant quantities ![]() or
or ![]() in the physical situations in which the old theory is valid, in particular in the Poincaré vacuum. As a matter of fact, it is impossible to find an expression that replaces
in the physical situations in which the old theory is valid, in particular in the Poincaré vacuum. As a matter of fact, it is impossible to find an expression that replaces ![]() , because it is odd under space inversion (represented by
, because it is odd under space inversion (represented by ![]() ) while the Poincaré structure constants are invariant under space inversion. Instead, a very natural replacement for
) while the Poincaré structure constants are invariant under space inversion. Instead, a very natural replacement for ![]() can be found in terms of the spinor
can be found in terms of the spinor ![]() defined in Section 3.7 by eq. (3.89). If we replace only
defined in Section 3.7 by eq. (3.89). If we replace only ![]() , we obtain a Lagrangian symmetric with respect to the subgroup of
, we obtain a Lagrangian symmetric with respect to the subgroup of
![]() that leaves
that leaves ![]() invariant, namely the axial symplectic group
invariant, namely the axial symplectic group
![]() introduced in Section 3.6. It is possible that theories invariant with respect to
introduced in Section 3.6. It is possible that theories invariant with respect to
![]() or
or
![]() , can be found in a more general geometric scheme, but some new idea is necessary.
, can be found in a more general geometric scheme, but some new idea is necessary.
Actually, in the construction of Lagrangians symmetric with respect to
![]() it is convenient to use the 5-vector
it is convenient to use the 5-vector ![]() defined by eq. (3.93) instead of the 6-vector
defined by eq. (3.93) instead of the 6-vector ![]() equivalent to the antisymmetric spinor
equivalent to the antisymmetric spinor ![]() , because we have
, because we have ![]() in all the theories cosidered in Chapter 5. With this choice, the substitution rule takes thye form
in all the theories cosidered in Chapter 5. With this choice, the substitution rule takes thye form
| (7.6) |
This substitution tends to an equality in the limit
| (7.7) |
The substitution rule can also be treated in a more abstract and general way, also working for the matter fields. We indicate by ![]() all the geometric objects and the other dynamical fields on which the Lagrangian
all the geometric objects and the other dynamical fields on which the Lagrangian ![]() depends and by
depends and by ![]() the representation of
the representation of
![]() acting on them. A normal Lagrangian form
acting on them. A normal Lagrangian form ![]() of the kind treated in Chapter 5 has the Lorentz invariance property
of the kind treated in Chapter 5 has the Lorentz invariance property
| (7.10) |
| (7.11) |
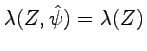 and
and
| (7.12) |
We can also apply the substitution rule to other Lorentz invariant expressions, to be used as building blocks in the construction of invariant Lagrangians. In particular starting from the 4-form ![]() defined in Section 0.3 one obtains
defined in Section 0.3 one obtains
| (7.13) |
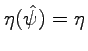 .
.
We shall also use the 3-forms
| (7.14) |
| (7.15) |