Many quantization procedures start from some kind of canonical formalism. A covariant canonical formalism on a group manifold has been developed in refs. [89,90]. A covariant symplectic approach to geometric field theories proposed in ref. [91] can be adapted very naturally to the theories described in the present notes and we shall follow many of its ideas, that will play an important role in the following. The symplectic structure of the phase space is the starting point of geometric quantization [67,68]. Though we have no reasonable hope to carry out the whole quantization of the classical theories we are considering, the general concepts given in the present Section may suggest some useful ideas.
It is useful to start from the analogy with a mechanical system with ![]() degrees of freedom [92,93,94]. The phase space
degrees of freedom [92,93,94]. The phase space ![]() can be interpeted as the space of motions, namely the space of the solutions of the equations of motion or of the corresponding initial conditions at a given time
can be interpeted as the space of motions, namely the space of the solutions of the equations of motion or of the corresponding initial conditions at a given time ![]() . We indicate by
. We indicate by ![]() ,
,
![]() a local system of Lagrangian coordinates, by
a local system of Lagrangian coordinates, by ![]() the corresponding velocities and we define, as usual, the canonical momenta
the corresponding velocities and we define, as usual, the canonical momenta
We use the symbol ![]() to denote the exterior derivative of differential forms defined on
to denote the exterior derivative of differential forms defined on ![]() , in order to avoid confusion with the exterior derivative of differential forms defined on
, in order to avoid confusion with the exterior derivative of differential forms defined on ![]() , that we continue to indicate by
, that we continue to indicate by ![]() . We also introduce the notation
. We also introduce the notation ![]() and
and 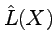 for the inner product and the Lie derivative acting on the differential forms in
for the inner product and the Lie derivative acting on the differential forms in ![]() . For the exterior product, we use in both cases the symbol
. For the exterior product, we use in both cases the symbol ![]() .
.
In the following it is useful to consider double differential forms, a concept treated with some detail in ref. [95]. A ![]() -double form defined, for instance, on
-double form defined, for instance, on
![]() is given, at a given point of this manifold, by a multilinear form depending (antisymmetrically) on
is given, at a given point of this manifold, by a multilinear form depending (antisymmetrically) on ![]() vectors of the tangent space of
vectors of the tangent space of ![]() and
and ![]() vectors of the tangent space of
vectors of the tangent space of ![]() . The manifold
. The manifold ![]() can be replaced by the manifold that describes the geometry in other theories, for instance the spacetime
can be replaced by the manifold that describes the geometry in other theories, for instance the spacetime ![]() or, in the simple mechanical system we are now considering, the time axis
or, in the simple mechanical system we are now considering, the time axis ![]() .
.
The time evolution of the system is described by a one-parameter group of diffeomorphisms of ![]() generated by a vector field
generated by a vector field ![]() . The dynamical variables are functions defined on
. The dynamical variables are functions defined on
![]() , that we can also consider as
, that we can also consider as ![]() -double differential forms. Their time derivative is given by
-double differential forms. Their time derivative is given by
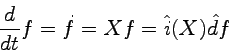 |
(4.75) |
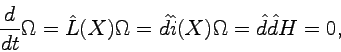 |
(4.77) |
We can consider ![]() as a double
as a double ![]() -form on the manifold
-form on the manifold
![]() . More explicitly, it is at the same time a 2-form on
. More explicitly, it is at the same time a 2-form on ![]() and a 0-form (namely a function) on
and a 0-form (namely a function) on ![]() . The fact that it does not depend on
. The fact that it does not depend on ![]() can be written as
can be written as ![]() , while
, while
![]() means that, for any value of
means that, for any value of ![]() , it is a closed form on
, it is a closed form on ![]() .
.
If we consider a field theory, the space ![]() is infinite-dimensional and the mathematics of differential forms [27] becomes rather delicate and also ambiguous, because one has to choose a norm, or at least a topology, in the tangent spaces. We shall not enter into these details and our proposal is admittedly deprived of any mathematical rigour. We hope that, if necessary, it will be possible to transform it into a mathematically acceptable treatment.
is infinite-dimensional and the mathematics of differential forms [27] becomes rather delicate and also ambiguous, because one has to choose a norm, or at least a topology, in the tangent spaces. We shall not enter into these details and our proposal is admittedly deprived of any mathematical rigour. We hope that, if necessary, it will be possible to transform it into a mathematically acceptable treatment.
Following the analogy with a mechanical system we treat the quantities
![]() and
and ![]() as ``Lagrangian coordinates'' and the quantities
as ``Lagrangian coordinates'' and the quantities
![]() and
and
![]() as the ``velocities''. A comparison between the normal field equations written in the form (4.29), (4.31) and eq. (4.73) suggests that the forms
as the ``velocities''. A comparison between the normal field equations written in the form (4.29), (4.31) and eq. (4.73) suggests that the forms
![]() and
and ![]() should be considers as the ``canonical momenta'' of the theory.
should be considers as the ``canonical momenta'' of the theory.
A natural generalization of eq. (4.74) is
The choice of ![]() is a difficult problem, but fortunately we can prove that, as a consequence of the field equations, we have
is a difficult problem, but fortunately we can prove that, as a consequence of the field equations, we have ![]() . As in the mechanical case, this is the crucial property of
. As in the mechanical case, this is the crucial property of ![]() . It follows that
. It follows that
![]() is not affected by deformations of
is not affected by deformations of ![]() that modify only a compact subset and not its boundary
that modify only a compact subset and not its boundary
![]() . However,
. However, ![]() should extend to infinity and problems of convergence may arise. Moreover,
should extend to infinity and problems of convergence may arise. Moreover,
![]() could depend on the asymptotic behavior of
could depend on the asymptotic behavior of ![]() .
.
It has been remarked, in the framework of quantum field theory [96,97], that globally defined quantities are not really observable and that a field theory should be described in terms of local algebras of observables concerning compact regions of spacetime. Perhaps the form
![]() with sufficiently large but compact
with sufficiently large but compact ![]() could be sufficient for the construction, by means of some quantization procedure, a local algebra of observables. A further development of this idea is completely outside the purposes of the present notes. In the following we do not specify the choice of
could be sufficient for the construction, by means of some quantization procedure, a local algebra of observables. A further development of this idea is completely outside the purposes of the present notes. In the following we do not specify the choice of ![]() , since many local results can be obtained by considering the symplectic double form
, since many local results can be obtained by considering the symplectic double form ![]() , without any reference to the symplectic form
, without any reference to the symplectic form
![]() .
.
The infinitesimal variations indicated by ![]() in the preceding Sections can be described by an infinitesimal vector field
in the preceding Sections can be described by an infinitesimal vector field ![]() defined on
defined on ![]() . If
. If ![]() is a dynamical variable, described as a
is a dynamical variable, described as a ![]() -double form, its infinitesiamal variation previously indicated by
-double form, its infinitesiamal variation previously indicated by ![]() , in the present Section should be indicated by
, in the present Section should be indicated by
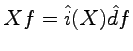 .
.
The 3-form ![]() defined by eq. (4.39) depends on a vector field
defined by eq. (4.39) depends on a vector field ![]() that describes the variations indicated by the symbol
that describes the variations indicated by the symbol ![]() and it is more correctly interpreted as a (1, 3)double form defined by
and it is more correctly interpreted as a (1, 3)double form defined by
| (4.80) |
| (4.81) |
| (4.82) |
| (4.83) |
Many interesting theories are described by a degenerate Lagrangian and one can eliminate (locally) the ``velocities''
![]() ,
,
![]() from the the normal equations (4.29) and (4.31), obtaining primary Lagrangian constraints that involve only the ``Lagrangian coordinates''
from the the normal equations (4.29) and (4.31), obtaining primary Lagrangian constraints that involve only the ``Lagrangian coordinates''
![]() ,
, ![]() and the ``canonical momenta''
and the ``canonical momenta''
![]() and
and ![]() . In some cases, from the other field equations one also obtains secondary constraints. As a consequence, the states of the system are described by the points of the submanifold
. In some cases, from the other field equations one also obtains secondary constraints. As a consequence, the states of the system are described by the points of the submanifold
![]() defined by all the constraint equations. A more detailed dicussion of primary and secondary constraints can be found, for instance, in ref. [98]. It may be useful to remark that the submanifold
defined by all the constraint equations. A more detailed dicussion of primary and secondary constraints can be found, for instance, in ref. [98]. It may be useful to remark that the submanifold ![]() is not necessarily defined by a set of global constraint equations. It may be necessary to use different constraint equations in a neighborhoods of differnt points of
is not necessarily defined by a set of global constraint equations. It may be necessary to use different constraint equations in a neighborhoods of differnt points of ![]() .
.
The symplectic formalism allows a treatment of the constraints considerably simpler than the better known approach based on the Poisson and Dirac brackets [98]. If the restriction
![]() of the form
of the form
![]() to the submanifold
to the submanifold ![]() is nondegenerate,
is nondegenerate, ![]() is a symplectic manifold to be identified with the phase space of the system. The corresponding Poisson brackets (different from the Poisson brackets of
is a symplectic manifold to be identified with the phase space of the system. The corresponding Poisson brackets (different from the Poisson brackets of ![]() ) are called the Dirac brackets.
) are called the Dirac brackets.
However, in the most interesting cases the 2-form
![]() is degenerate. In this case, the space
is degenerate. In this case, the space ![]() is not a symplectic space, but a pre-symplectic space and there are vector fields
is not a symplectic space, but a pre-symplectic space and there are vector fields ![]() on
on ![]() that satisfy the condition
that satisfy the condition
| (4.84) |
| (4.85) |
Alternatively (under suitable conditions), one can introduce, besides the Lagrangian constraints, other gauge fixing constraints that define a submanifold
![]() that itersects all the leaves of
that itersects all the leaves of ![]() at only one point and is clearly equivalent to the set of the leaves introduced above. In this case, one can identify
at only one point and is clearly equivalent to the set of the leaves introduced above. In this case, one can identify
![]() with the restriction of
with the restriction of
![]() to
to ![]() . We can also consider the restriction
. We can also consider the restriction
![]() of the 1-form
of the 1-form
![]() to
to ![]() and we have
and we have
| (4.86) |
However, it is not always possible to find a submanifold ![]() with the required properties, as one can see from simple finite-dimensional examples. Then the closed form
with the required properties, as one can see from simple finite-dimensional examples. Then the closed form
![]() does not need to be exact and may have nontrivial topological (cohomological) properties that can give rise to obstructions to the quantization procedure [67,68] unless the Planck constant
does not need to be exact and may have nontrivial topological (cohomological) properties that can give rise to obstructions to the quantization procedure [67,68] unless the Planck constant ![]() takes some special values, as we have shortly discussed in Section 2.4. It is for this reason that we try to give some attention to the topological properties of the phase space.
takes some special values, as we have shortly discussed in Section 2.4. It is for this reason that we try to give some attention to the topological properties of the phase space.
We have already remarked in Section 2.5 that the theories we are considering have gauge transformations corresponding to the diffeomorphisms of ![]() . If the vector field
. If the vector field ![]() in
in ![]() generates infinitesimal diffeomorphisms of this manifold, the vector field
generates infinitesimal diffeomorphisms of this manifold, the vector field ![]() on
on ![]() that generates the corresponding gauge transformations is defined by
that generates the corresponding gauge transformations is defined by
| (4.87) |
| (4.88) |
By means of the formulas given above and eq. (4.43) and (4.51), we can write
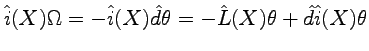 |
|||
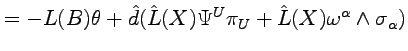 |
|||
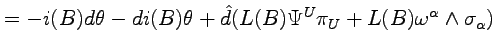 |
|||
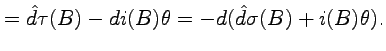 |
(4.89) |
| (4.90) |
If ![]() generates a symmetry transformation of the kind (2.11),
all the quantities that have only contracted indices are invariant and in particular we have
generates a symmetry transformation of the kind (2.11),
all the quantities that have only contracted indices are invariant and in particular we have
| (4.91) |
| (4.92) |
| (4.93) |
As a further application of the double forms, we consider the addition to the Lagrangian form of an exact term of the kind ![]() , where the 3-form
, where the 3-form ![]() depends only on
depends only on
![]() and
and ![]() , namely on the ``Lagrangian coordinates'', but not on the ``velocities''. We know that the field equations remain unchanged. We have
, namely on the ``Lagrangian coordinates'', but not on the ``velocities''. We know that the field equations remain unchanged. We have
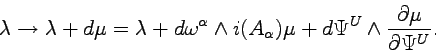 |
(4.94) |
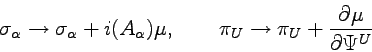 |
(4.95) |
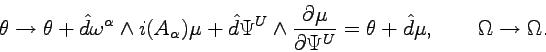 |
(4.96) |
If the vector field ![]() defined on
defined on ![]() generated a symmetry transformation leaving the Lagrangian invariant, for the corresponding conserved quantity
generated a symmetry transformation leaving the Lagrangian invariant, for the corresponding conserved quantity ![]() we have
we have
| (4.97) |