Two examples of Lagrangians invariant under $Sp(4, \mathbf{R})_A$.

In ref. [6] two Lagrangians with $Sp(4, \mathbf{R})_A$ symmetry have been suggested, showing that the corresponding theories have the Poincaré vacuum solution, besides the degenerate vacuum solutions obtained from it by the action of the symmetry group. The existence of nonvacuum solutions was not investigated, due to mathematical difficulties, and in the present Chapter we continue this study using the concepts developed in the preceding Sections. We find that these models are not completely satisfactory, but they provide a basis for the construction of more acceptable theories.

We use the conventions we have adopted in the present notes and the 5-dimensional tensor calculus for $SO(2, 3)_V$ described in Section 3.6. In particular we use the 5-vectors $f_u$, $\psi_u$ defined by eqs. (3.93), (7.5) and the notation $\omega^{[uv5]}$ for the 1-forms $\omega^{\alpha}$, in analogy with eq. (3.69). The index $5$ is added for compatibility with the 6-dimensional formalism and to recall that the other two indices take the values $u, v = 0,\ldots, 4$ and transform according to $SO(2, 3)_A$.

The first Lagrangian is

$$\lambda^H = - 2 \ell^2 k \psi_x \psi_y g_{uu'} g_{vv'} d \omega^{[uv5]} \wedge \omega^{[xu'5]} \wedge \omega^{[yv'5]},$$

$$\lambda^A = \ell^2 k \psi_x \psi_y \psi^z g_{uu'} \epsilon_{vv'ww'z}... ...a^{[ww'5]} \wedge \omega^{[uv5]} \wedge \omega^{[xu'5]} \wedge \omega^{[yv'5]}.$$ (7.42)

It contains the fields $\psi_u$, but not the field $\phi$ and the normal equation (7.28) is trivially satisfied. We have seen in Section 7.2 that the normal equation (7.27) is equivalent to the conservation of $\theta_{[uv]}$ and we do not need to consider it. If the normal field equations are satisfied, we have

$$\sigma_{[uv5]} = - 4 \ell^2 k \psi_x \psi_y g_{uu'} g_{vv'} \omega^{[xu'5]} \wedge \omega^{[yv'5]}.$$ (7.43)

In order to find the primary constraints, we have to express the quantity $\psi_x \psi_y$, that contains the structure coefficients, in terms of the ``canonical momenta.'' From eq. (7.43) we have

$$g^{uu'} g^{vv'} i(A_{[xu'5]}) i(A_{[yv'5]}) \sigma_{[uv5]} = 24 \ell^2 k \psi_x \psi_y$$ (7.44)

and the pre-symplectic double form can be written as

$$\Omega' = - \hat d \theta' = - 2 \ell^2 k g_{uu'} g_{vv'} \... ...\hat d (\psi_x \psi_y \omega^{[xu'5]} \wedge \omega^{[yv'5]}),$$ (7.45)

$$\theta' = - 2 \ell^2 k \psi_x \psi_y g_{uu'} g_{vv'} \hat d \omega^{[uv5]} \wedge \omega^{[xu'5]} \wedge \omega^{[yv'5]}.$$ (7.46)

One can see that for 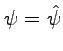$\psi = \hat \psi$ the Lagrangian (7.42) coincides with the Regge-Ne'eman Lagrangian given in eqs. (5.1) and (5.2) with $k_1 = k_2 = k_4 = 0$ and $k_3 = k$ and the pre-symplectic form (7.45) coincides with eq. (6.63). It follows that the model we are considering can be obtained from the Regge-Ne'eman Lagrangian by means of the substitution rule.

The conserved 3-forms (7.32) are

$$\theta^G_{[uv]} = \hat i (X_{[uv]}) \theta' = g_{vw} \omega^{[ww'5]} \wedge \sigma_{[uw'5]} - g_{uw} \omega^{[ww'5]} \wedge \sigma_{[vw'5]}$$

$$= - 4 \ell^2 k \psi_x \psi_y (g_{uu'} g_{vv'} - g_{uv'} g_{vu'}) g_{ww'} \omega^{[v'w5]} \wedge \omega^{[xu'5]} \wedge \omega^{[yw'5]}.$$ (7.47)

An important consequence is

$$\psi^u \theta^G_{[uv]} = 0$$ (7.48)

showing that a solution of the Einstein-Cartan theory is also a solution of the theory we are considering if and only if $d \theta^M_{[4k]} = 0$. From eqs. (4.69) and (5.49) we obtain

$$\theta^M_{[4k]} = W^5 \eta_k, \qquad d \theta^M_{[4k]} = (A... ...kj}^j W^5) \eta + \phi W^5 g_{kn} \omega^{[mn]} \wedge \eta_m.$$ (7.49)

In the model we are considering we have $F_{kj}^j = 0$ and $\phi = 1$, but these terms are necessary in the second model. We see that the condition is simply $W^5 = 0$.

From the conservation law (7.32) we obtain

$$d \psi^u \wedge \theta^G_{[uv]} = \psi^u d \theta^M_{[uv]}.$$ (7.50)

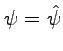and we see that if the 5-vector $\psi^u$ is constant, the right hand side must vanish. In order to discuss this equation with more detail, we choose an adapted basis in $T_{\hat s} \mathcal{S}$, so that at the particular point $\hat s$ we have $\psi = \hat \psi$ and therefore, in the 4-dimensional Lorentz formalism,

$$\theta^G_{[4i]} = 0, \qquad \theta^G_{[ik]} = 2k (g_{ij} \e... ...psilon_{ilmn}) \omega^{[mn]} \wedge \omega^j \wedge \omega^l,$$ (7.51)

$$d \psi^i \wedge \theta^G_{[ik]} = 4 k (g_{im} \delta_k^p \delta_n^q ... ...elta_n^q - g_{kn} \delta_i^q \delta_m^p) A_p \psi^i \omega^{[mn]} \wedge \eta_q$$

$$+ k (g_{ij} \epsilon_{klmn} - g_{kj} \epsilon_{ilmn}) A_{[pq]} \psi^i \omega^{[pq]} \wedge \omega^{[mn]} \wedge \omega^j \wedge \omega^l.$$ (7.52)

In the absence of Fermion fields, this expression must vanish and, after some calculations, we find that the derivatives of $\psi_i$ must vanish too. If this happens in a connected region of $\mathcal{S}$, in this region we have $\psi_i = 0$ and all the equations coincide with the ones examined in Chapter 5. It is interesting to consider a situation in which the Fermion fields are very small and therefore $\psi_i$ is very small too and eq. (7.49) has an approximate validity. A comparison of the preceding equations gives the approximate results, valid in an adapted frame,

$$A_k W^5 = 0, \qquad A_{[ik]} \psi_j = 0, \qquad A_i \psi_k = (2 k)^{-1} W^5 g_{ik}.$$ (7.53)

From this equation we learn that the quantity $W^5$, related to the Fermion spin, is responsible for the appearance of nonvanishing (or nonconstant) values of $\psi_i$. If in a connected region $W^5 = 0$, the theory is perfectly equivalent to the Einstein-Cartan theory. We shall see in Chapter 9 that $W^5$ is extremely small if one excludes the interior of stars and the first few minutes of the big bang. It follows that the model presented in the present Section is in agreement with the observations.

Unfortunately, eq. (7.53) shows that $W^5$ must be a constant and this in an unacceptable condition on the Fermion fields. We conclude that the model is (at least) incomplete and that other gravitatinal degrees of freedom must be introduced in order to obtain a correct matching of the two sides of eq. (7.50). The first candidates are the fields $\chi_{\alpha}$ defined in eq. (7.18), as we discuss in the following Section.

The second Lagrangian proposed in ref. [6], symmetric under total dilatations as in eq. (6.55), is

$$\lambda^H = - 2^{-1} \ell^2 \phi^{m-1}(\psi_x \psi_y + (m - 1)^{-1} ... ...g_{uu'} g_{vv'} d \omega^{[uv5]} \wedge \omega^{[xu'5]} \wedge \omega^{[yv'5]},$$

$$\lambda^A = 2^{-2} \ell^2 \phi^m \psi_x \psi_y \psi^z g_{uu'} \epsil... ...'5]} \wedge \omega^{[uv5]} \wedge \omega^{[xu'5]} \wedge \omega^{[yv'5]}. \quad$$ (7.54)

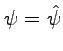One can see that for $\psi = \hat \psi$ it coincides with the Lagrangian studied in Sections 6.1 and 6.2 with

$$k = 2^{-2} \phi^{m - 1}, \qquad k_1 = 2^{-2} (m - 1)^{-1} \phi^{m - 1},$$

$$k_2 = - \ell^2 k_1, \qquad k_3 = 2^{-2} \phi^m, \qquad k_4 = k_5 = 0.$$ (7.55)

Note that the field $\phi$ is defined in a different way. If we also take the limit $\ell \to 0$, we obtain the model of Section 6.2 without the cosmological term and the Lagrangian $\lambda^{\chi}$ proportional to $k_5$. We have shown in Section 6.1 that a model with $k_5 = 0$ has problems if massive particles are present and is, in any case, in disagreement with observations that suggest a very large value of the parameter $\omega$.

In analogy with the first model, we have

$$\sigma_{[uv5]} = - \ell^2 \phi^{m-1} (\psi_x \psi_y + (m - 1... ...{xy}) g_{uu'} g_{vv'} \omega^{[xu'5]} \wedge \omega^{[yv'5]},$$ (7.56)

$$\theta^G_{[uv]}= - \ell^2 \phi^{m-1} \psi_x \psi_y (g_{uu'} ... ... \omega^{[v'w5]} \wedge \omega^{[xu'5]} \wedge \omega^{[yw'5]}$$ (7.57)

and eqs. (7.48) and (7.50) are valis also in this case.

It is interesting to examine, as in the first model, the approximate explicit form of eq. (7.50) for small values of $W^5$ and of $\psi_i$ and we obtain

$$A_k W^5 = F_{kj}^j W^5, \qquad A_{[ik]} \psi_j = 0, \qquad A_i \psi_k = 2 \phi^{1-m} W^5 g_{ik}.$$ (7.58)

In this approximation the scalar-tensor theory of Sections 6.1 and 6.2 is approximately valid an we can use, eq. (6.41) to obtain the relation

$$A_k \ln W^5 = F_{kj}^j = - \omega A_k \ln \Phi, \qquad \Phi = C (W^5)^{- 1/ \omega}.$$ (7.59)

where $C$ is a constant. This means that in an empty region, where $W^5 \to 0$, we have $\Phi \to \infty$ or $\Phi \to 0$, according to the sign of $\omega$. This unacceptable feature can be avoided only if $1/ \omega \to 0$ (as it is suggested by the astronomical observations) namely if $\alpha = 1/3$. In the model we are considering, without the additional term (6.3), we have $\alpha = 0$ and $\omega = - 3/2$. This argument suggests that we have to add to the Lagrangian the additional term (6.3) with the appropriate coefficient.