A treatment of matter fields is given in refs. [4,5,102], where fields with arbitrary spin are considered. In the present notes we treat only scalar and Dirac fields, which are needed in the Standard Model of elementary particles [41] to describe the Higgs field and Fermions, namely we put
![]() . We try, as far as it is possible in a classical framework, to take into account some special features of the Standard Model, in particular the chiral character of the internal gauge transformation of Fermions and the mass generation mechanism.
. We try, as far as it is possible in a classical framework, to take into account some special features of the Standard Model, in particular the chiral character of the internal gauge transformation of Fermions and the mass generation mechanism.
The word ``scalar'' has two different meanings. From a first point of view, a scalar field is invariant under the Lorentz transformations considered as elements of the structural group of a principal fibre bundle. This property will appear as a consequence of the field equations. From another point of view, it is invariant with respect to the Lorentz transformations considered as elements of the symmetry group ![]() of the Lagrangian and of the field equations.
of the Lagrangian and of the field equations.
We describe the real scalar fields of the theory by the one-column matrix ![]() , on which an orthogonal representation of the internal symmetry group operates. A complex scalar field can be decomposed in its real and imaginary parts, that appear as different elements of the one-column matrix
, on which an orthogonal representation of the internal symmetry group operates. A complex scalar field can be decomposed in its real and imaginary parts, that appear as different elements of the one-column matrix ![]() . We indicate by
. We indicate by ![]() the real antisymmetric matrices that describe the infinitasimal internal symmetry transformations of this group.
the real antisymmetric matrices that describe the infinitasimal internal symmetry transformations of this group.
The field equations can be derived from the Lagrangian form [4,5,102]
The dericatives of ![]() appear only in
appear only in ![]() and we have
and we have
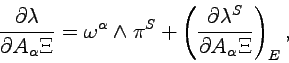 |
(5.27) |
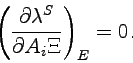 |
(5.29) |
After some calculations, we obtain the normal field equations in the more explicit form
If we use the normal field equations, the Lagrangian (5.26) takes the form
| (5.32) |
| (5.33) |
| (5.34) |