Orbits in
The action of
![]() on the linear space
on the linear space ![]() splits it into orbits, that, according to Sylvester's law of inertia, are characterized by the numbers
splits it into orbits, that, according to Sylvester's law of inertia, are characterized by the numbers ![]() and
and ![]() of the positive and negative eigenvalues of the matrix
of the positive and negative eigenvalues of the matrix ![]() . We indicate these orbits by
. We indicate these orbits by
![]() with
with ![]() . We have
. We have
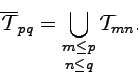 |
(3.38) |
If we fix the quantities
![]() , the fourth degree equation (3.39) determines four real values of
, the fourth degree equation (3.39) determines four real values of ![]() , that divide the real axis into five open (possibly empty) intervals, corresponding to the five open orbits. When
, that divide the real axis into five open (possibly empty) intervals, corresponding to the five open orbits. When ![]() , two roots tend to
, two roots tend to
![]() and the other two roots tend to
and the other two roots tend to
![]() . As a consequence, the open orbits (or their closures) tend to the following limits
. As a consequence, the open orbits (or their closures) tend to the following limits
For ![]() , the causal structure of
, the causal structure of ![]() is more complicated and its physical interpretation is not evident. A discussion of this problem is given in refs. [12,14]. The interpretation of
is more complicated and its physical interpretation is not evident. A discussion of this problem is given in refs. [12,14]. The interpretation of
| (3.41) |
The cone ![]() defines a partial ordering in
defines a partial ordering in ![]() . If
. If ![]() is flat, namely it is an affine space and all the vector fields
is flat, namely it is an affine space and all the vector fields ![]() commute, we can define the ``difference'' operation
commute, we can define the ``difference'' operation
![]() . Then the order relation
. Then the order relation ![]() is defined by
is defined by
| (3.42) |
We try an interpretation of the other orbits only when ![]() is flat. This is a good approximation if we consider a sufficiently small region of
is flat. This is a good approximation if we consider a sufficiently small region of ![]() . In Chapter 11 (see also [12]) we show that the free quantum field operators
. In Chapter 11 (see also [12]) we show that the free quantum field operators ![]() and
and ![]() defined in the flat space
defined in the flat space ![]() commute if
commute if
![]() . In analogy with the quantum field theories in Minkowski spacetime, we say that in this case the points
. In analogy with the quantum field theories in Minkowski spacetime, we say that in this case the points ![]() and
and ![]() are causally disjoint, namely there is no causal influence between them.
are causally disjoint, namely there is no causal influence between them.
Of course, we have to clarify the concept of causal influence and this requires the discussion of a kind of procedures that generalize the measurement and the transformation procedures discussed in Section 2.2. We call them restricted measurement procedures and they have the aim, starting from a local frame ![]() , of measuring some observables and to build a new local frame
, of measuring some observables and to build a new local frame ![]() . A class of equivalent restricted measurement procedure is called a restricted measurement. Of course, we must have
. A class of equivalent restricted measurement procedure is called a restricted measurement. Of course, we must have ![]() .
.
The result of the restricted measurement is available at the frame ![]() , in the sense that it can be used to specify some detail of a new procedure performed starting from
, in the sense that it can be used to specify some detail of a new procedure performed starting from ![]() . We say that the restricted measurement starts at
. We say that the restricted measurement starts at ![]() and ends at
and ends at ![]() . We have already observed in Section 2.6 that it is not reasonable to assume that the result of a measurement performed in a local frame is available immediately to be used in procedures starting from the same frame. The result of an unrestricted measurement is available only after a macroscopic time, to be registered by some macroscopic instrument.
. We have already observed in Section 2.6 that it is not reasonable to assume that the result of a measurement performed in a local frame is available immediately to be used in procedures starting from the same frame. The result of an unrestricted measurement is available only after a macroscopic time, to be registered by some macroscopic instrument.
We say that a local frame ![]() is causally influenced by a local frame
is causally influenced by a local frame ![]() if a procedure starting at
if a procedure starting at ![]() can influence the result of a restricted measurement ending at
can influence the result of a restricted measurement ending at ![]() . One cannot justify the assumption that this relation is transitive, because the information transmitted from
. One cannot justify the assumption that this relation is transitive, because the information transmitted from ![]() to
to ![]() is not necessarily of the kind that can be transmitted from
is not necessarily of the kind that can be transmitted from ![]() to
to ![]() .
.
We assume that ![]() is causally influenced by
is causally influenced by ![]() if
if
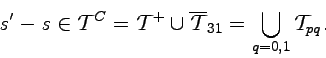 |
(3.43) |
| (3.44) |
If
| (3.46) |
The reciprocal influence replaces the spacetime coincidence of the normal relativistic theories in the same way as the spacelike separation of two events replaces in a relativistic theory the time coincidence (simultaneity) of the Newtonian theory. In a situation in which the light velocity can be considered as infinite, there is no observable difference between spacelike separation and simultaneity. In a similar way, in a situation in which one can disregard the fundamental length, there is no observable difference between reciprocal influence and spacetime coincidence.
Note that the relation of reciprocal influence (as well as the relation of spacelike separation) is not transitive and cannot be used to build equivalence classes, to be interpreted as points of spacetime (events).
From the property (3.37) we see that only the orbits
![]() and
and
![]() contain straight lines. The orbit
contain straight lines. The orbit
![]() also contains 3-dimensional vector subspaces, for instance the subspace generated by
also contains 3-dimensional vector subspaces, for instance the subspace generated by ![]() ,
, ![]() and
and ![]() . Though we have no proof, we conjecture that
. Though we have no proof, we conjecture that
![]() does not contain 4-dimensional vector subspaces.
does not contain 4-dimensional vector subspaces.
We say that a submanifold of ![]() is spacelike if all its tangent vectors belong to
is spacelike if all its tangent vectors belong to
![]() . We shall see in Section 4.1 that important physical quantities (conserved or not) are given by integrals of 3-forms on a 3-dimensional submanifold. It is natural to choose spacelike submanifolds, but a more restrictive choice may be necessary.
. We shall see in Section 4.1 that important physical quantities (conserved or not) are given by integrals of 3-forms on a 3-dimensional submanifold. It is natural to choose spacelike submanifolds, but a more restrictive choice may be necessary.